Observations show that ![]()
So we can use this to derive...
| ...the orbital period of the Sun... | 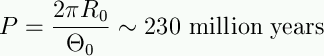 |
| ...and the mass of the Galaxy. | 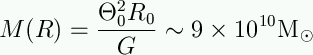 |
(Review Question: how did we get R0?)
This is somewhat more than the observed
mass in stars and gas, similar to what we found when we worked
out the local mass density of the disk using the Oort
Limit. So what's going on?
This analysis is only for the Sun's
galactocentric radius
(R0). Can we do this throughout the Galaxy and get
v(R)?
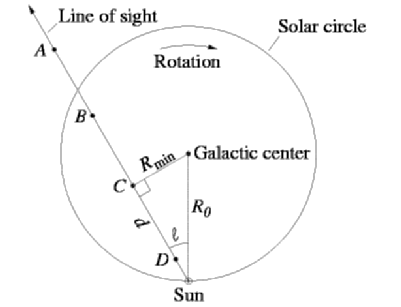
Imagine looking at some line of sight through the
galaxy
and observing the gas clouds:
 |
 |
|
|
|
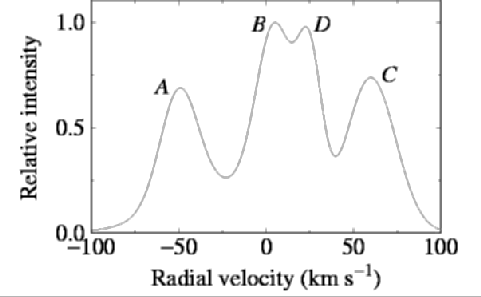
So v(C) = v(Rmin) = v(R0sin(l)).
| We can do this mapping for all
R<R0.
At R>R0, the geometry becomes ambiguous,
and we need to actually
know the true distance to whatever object we are
measuring the velocity
of. This is harder, although still possible.
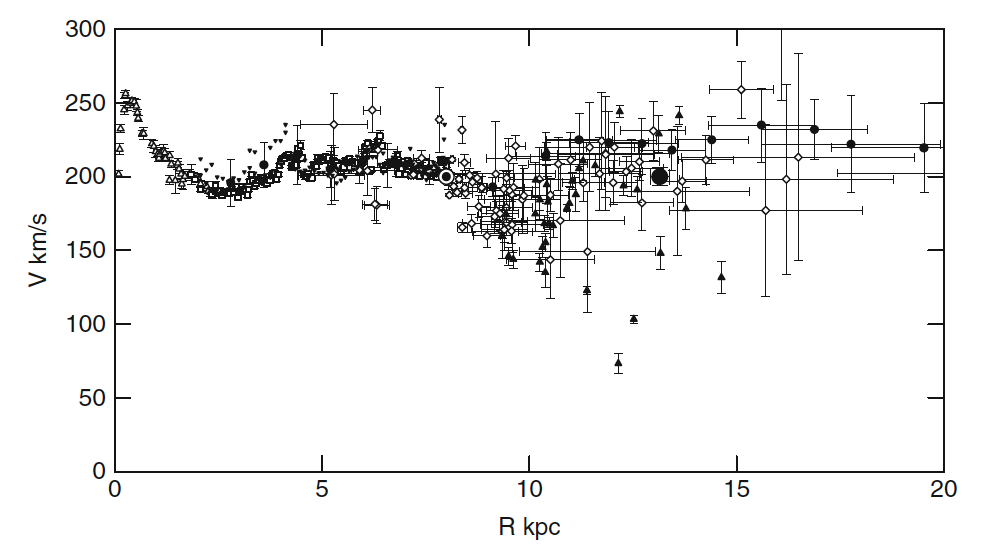
From this, we construct the rotation curve of the Milky Way (Sofue 2009): |
 |