The Velocity Distribution of Stars

---

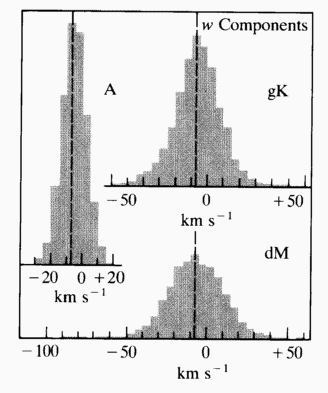
Make a histogram of the w (up/down) velocities of stars of different spectral type: A stars ("A") K giants ("gK") M dwarfs ("dM") (what is different about these groups of stars?) The spread in velocities -- called the velocity dispersion and calculated as the standard deviation of the distribution -- is different for each group: Stars Dispersion (km/s) A 9 gK 17 dM 18 white dwarfs 25

Remember also that different groups of stars had different disk thicknesses:
 
 

Question #1: Why does dispersion increase with spectral type?

Question #2: Why do dispersion and scale height increase together?

Disk Heating

The disk is not perfectly smooth -- there are "lumps" of matter (what kind of lumps?)

As stars move through these lumps, they scatter gravitationally, increasing their random velocities and moving from circular orbits to elliptical orbits. As a group, their velocity dispersion increases.

Why are they born on circular orbits?

The Oort Limit

Imagine the disk as a plane parallel slab of mass. Gravity pulls stars towards the disk, their velocities can carry them away. We want to balance these two effects:

First, think of balancing KE with PE for a small mass m orbiting a big mass M:
So we can solve for the big mass M:
Now, instead of a big mass M, think of a circular patch of  radius r and surface density  Sigma (in Msun/pc2). It has a total mass:
So plug that in and get
Or, now thinking about a group of stars:

So if we measure velocity dispersions and scale heights for groups of stars, we can measure the mass density of the Galaxy's disk. This was first done in the early 1930s by Jan Oort and is called the Oort limit. Modern analyses gives ~ 75 M_sun/pc² or so.

Now let's just add up all the mass we see:
 

Stars	30 Msun/pc2
Stellar remnants (mostly WDs)	5 Msun/pc2
Brown Dwarfs	2 Msun/pc2
Gas (HI+H2)	13 Msun/pc2
Total	50 Msun/pc2

Hmm. What's going on??