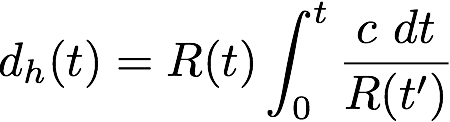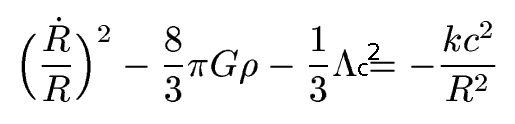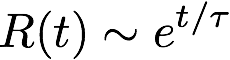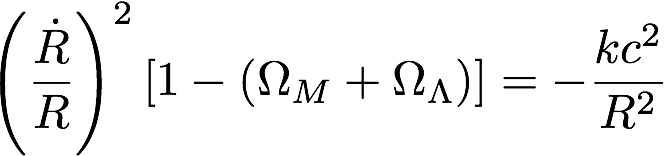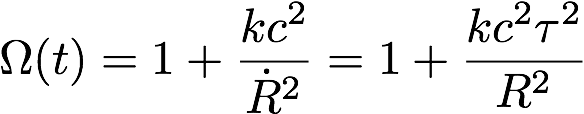Motivating Inflation

---

The flatness problem

Why is Omega_Total ~ 1? Why not 106? Why not 42? Why not 0.0021034011031?

The density of the Universe changes with time, as the Universe expands. So Omega_M, the ratio of the actual density to the critical density also changes:

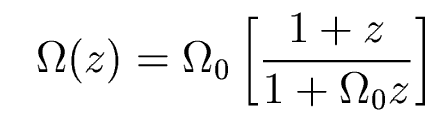
(Strictly speaking, this holds only for a matter dominated universe. But it's only recently that dark energy has started affecting the expansion of the universe, so early on the universe behaved like a matter dominated universe....)

Let's look at two examples.

• At a redshift of z=10,000 (ie when the universe was 10⁴ times smaller than now), it had a density parameter of 1.0001
• At a redshift of z=10,000, it had a density parameter of 0.9

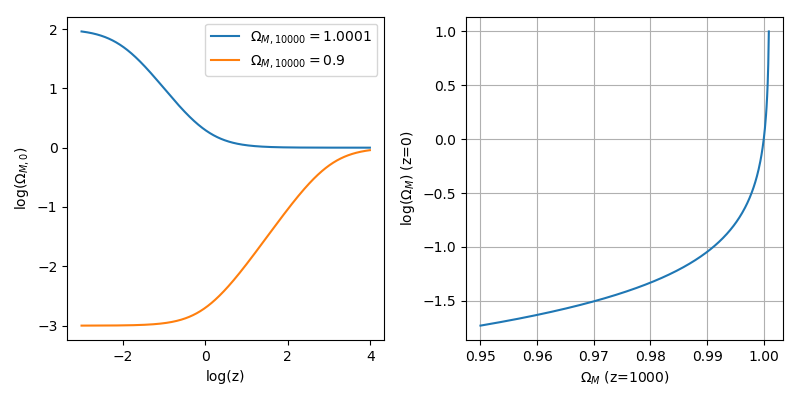
In the universe that is slightly overdense at z=10⁴, the density parameter today (at z=0) would be 100. In the universe that is slightly underdense at early times, we ought to measure a density parameter today of 0.001. Omega very quickly diverges from 1, unless it is equal to 1.

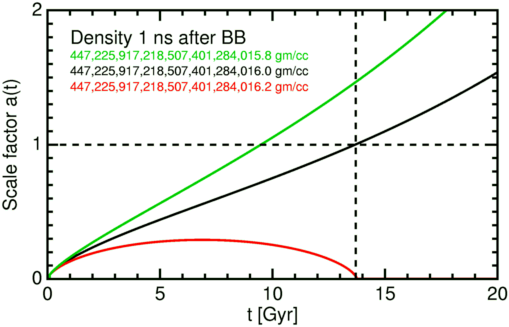
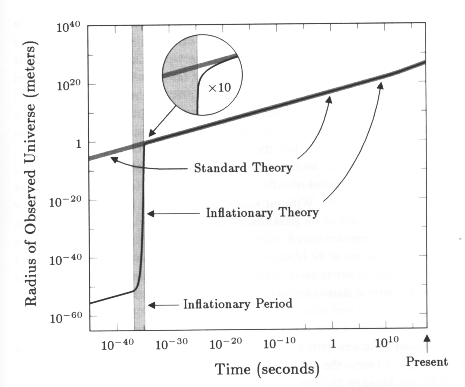
It gets worse. Look at this figure (from Ned Wright's Cosmology Tutorial): if the density of the universe had been ever so slightly non-critical 1 nanosecond after the big bang, we would have a drastically different universe:

The Horizon (or Smoothness) Problem

Looking at the microwave background, it is very smooth to 1 part in 10⁵. Everywhere. But at the time of recombination, regions of the universe which are now separated by more than 2 degrees on the sky were never in causal contact.

Think about the horizon distance:

At the time of the CMB, the horizon scale was about 0.25 Mpc. The current horizon distance is ~ 14.6 Gpc, so the observable universe at a redshift of z=1100 was 14.6 Gpc/1100 ~ 13.2 Mpc in size.

Therefore the angular size of a causally connected region at z=1100 is 0.25 Mpc / 13.2 Mpc = 0.02 radians ~ 1 degree.

So how did regions spanning the entire observable universe "know" that they should all be at exactly the same temperature?

Inflation

Remember the evolution of the universe dominated by cosmological constant. Given the Friedman equation:

if we are dominated by a cosmological constant, then we can ignore the matter term and solve for the evolution of the scale factor as

where tau is a characteristic e-folding timescale.

Inflation posits that such an exponential expansion happened in the early universe (but different from the current cosmological constant model).  At a time of 10^-24 seconds it expanded by a factor of 10⁵⁰. How would this fix the flatness and smoothness problems?
 
 
• flatness: imagining blowing up a globe by a factor of 10⁵⁰. Any curvature it had would be instantly "flattened". Quantitatively we can rewrite the Friedman equation in terms of OmegaM and OmegaL
  
  
  
  
  
  and then solve for OmegaT
  
  
  
  
  
  So if the expansion in size is 10⁵⁰, OmegaT=1.0 pretty much exactly. The post-inflation universe is flat.
  

• smoothness: originally the universe was smaller than the extrapolation of the standard expansion history to early epochs. So before inflation, everything was causally connected, then inflation drove things apart.




But what drives inflation?

We don't know.