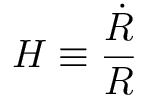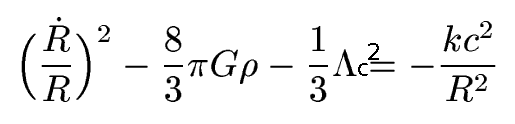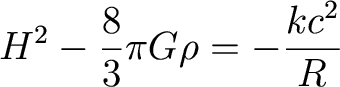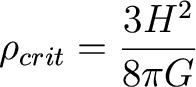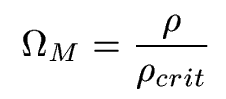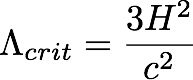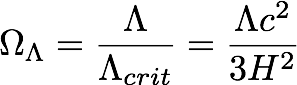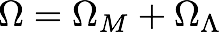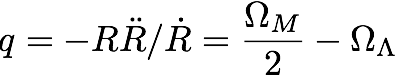Cosmological Parameters
Before going further, it is useful to
define some of the
cosmological parameters in the Friedmann equation (and elsewhere).
1. The Hubble Parameter
The Hubble
parameter is the normalized rate of expansion:
Note that the Hubble parameter is
not a constant! The Hubble constant
is the Hubble parameter measured today -- we denote
its value by H0. Current estimates are in the range
of H0 = 65-75 km/s/Mpc -- we will discuss these efforts in
more
detail later.
Also note you will often see the
parameter h,
particularly in distance-dependant quantities (for example, 75h-1
Mpc). This is usually defined by h=H0/100.
2. The Matter Density Parameter.
Look at the Friedmann
equation:
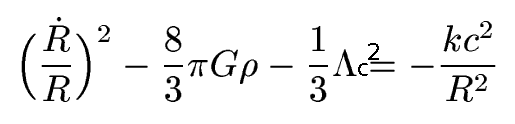
Rewriting this using the Hubble
parameter, and for now set Lambda=0:
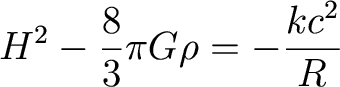
The Universe is flat if k=0, or if
it has a critical density
of
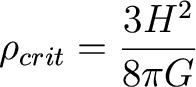
Remember,
this is not the density that the universe actually is, its the density
the universe would have to have if it was spatially flat by matter
alone.
We define the matter
density parameter to describe the actual density of the universe relative to this critical density:
So if Om=1, and there was no dark energy/lambda, the universe would be spatially flat. Best measurements for Om are about 0.25
- 0.35
3. The "dark energy"
density parameter
We can express a similar density
parameter for lambda again by using the Friedmann equation and setting
rhom=0. This gives us a "critical lambda" that would flatten the universe:
And then we can define the dark energy density parameter analogously to the matter density parameter:
So
if OL=1, and there was no matter, then the universe would be spatially flat. Best measurements for OL are about 0.65-0.75
4. "Total Omega"
What
is Total Omega if the Universe is flat? What is Total Omega if the Universe is
accelerating?
5. The deceleration parameter
Describes
the rate of change (de/acceleration) of the Universe's expansion: