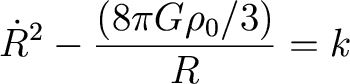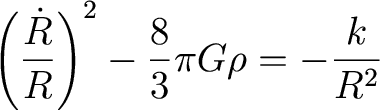The Dynamics of the Expanding Universe
We'll illustrate expansion dynamics
using Newtonian gravitational
dynamics.
Happily, the same dynamical equations come out of
general
relativity for a relativistic cosmology, with a few terms redefined.
Start with a test particle on the
surface of an
expanding
sphere of radius R. Its equation of motion is
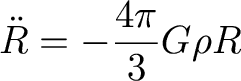 Since density is proportional to R-3,
and we
define
"now" with a 0 subscript, and R0=1, we have
Since density is proportional to R-3,
and we
define
"now" with a 0 subscript, and R0=1, we have
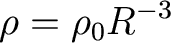 Which we can insert into the equation of
motion to get
Which we can insert into the equation of
motion to get
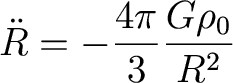
Note that
if rho0
is nonzero, the Universe must be expanding or contracting. It cannot be
static.
How do we integrate this? Multiply
both side by Rdot
to get
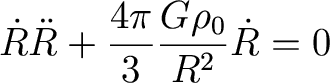 And remember that
And remember that
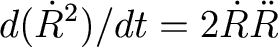 So that
So that
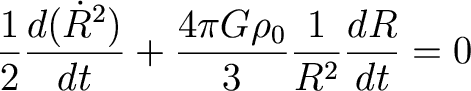
Now, also remember:
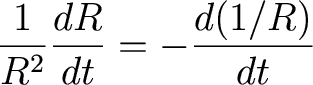
So that we have

 Or,
Or,
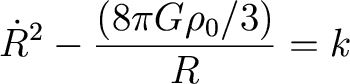
Replacing rho0 with rho,
and dividing by R2,
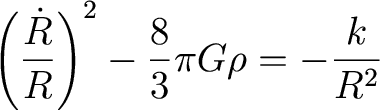
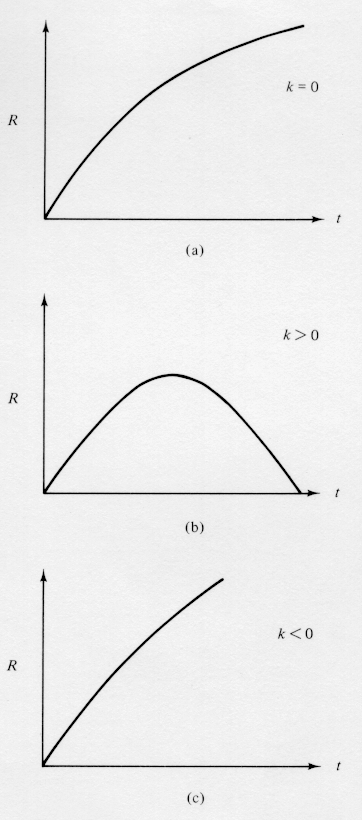
What does this mean?
- If k=0, then
Rdot is
always positive, and the expansion continues at an ever slowing pace
(since
rho is dropping). This is called a critical
or
flat universe.
- If k>0,
Rdot is initially
positive, but will reach a point where it changes sign. Expansion turns
into contraction. This is a closed universe.
- If k<0,
Rdot is always
positive, and never goes to zero -- expansion always continues. This is
an open universe.
Note: we are ignoring any cosmological constant here!
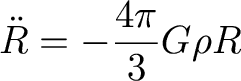
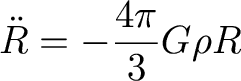
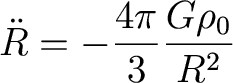
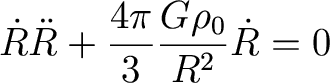
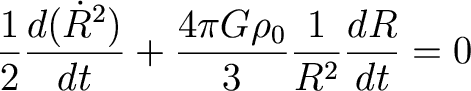
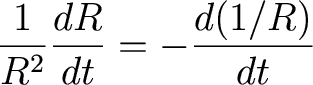

 Or,
Or,