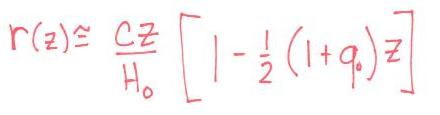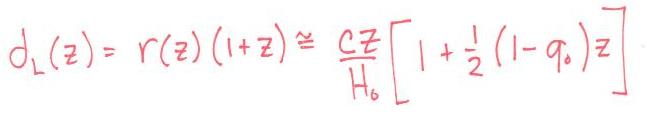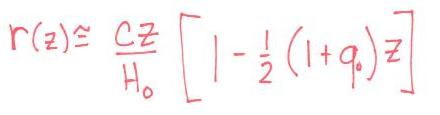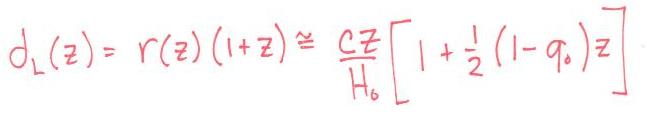The Extragalactic Distance Scale
What do we mean by distance?
Luminosity distance, angular size distance, etc all reduce to "normal"
geometric distances at low redshift (i.e., nearby universe). For small z, Taylor
expansion of comoving coordinate distance and luminosity distance, for example, looks like this:
and similar for dA(z), etc. so as z-->0, all these distances converge to cz/H0, or Hubble's law: v=H0d.
So why do we need to get this right?
Astrophysics:
- turn observed properties of objects (apparent
magnitude, angular size) into intrinsic properties of objects
(luminosity, physical size)
Measure H0:
- Cosmological parameter, want local, independent confirmation of cosmological measurements at high redshift.
- Once measured, can use it as a distance indicator (Hubble distance: d=v/H0)
Measure peculiar motions in the universe:
- vobs = H0d + vpec
- if we know distance independent of redshift, we can look for large scale velocity structure in the universe
Important Complications:
- An accurate measure of H0 means getting out to a distance where vpec<<H0d.
- Distances within clusters (ie with accuracies of +/- few Mpc) are not knowable via Hubble's law.
- Need several distance estimators to reduce systematic errors between methods.
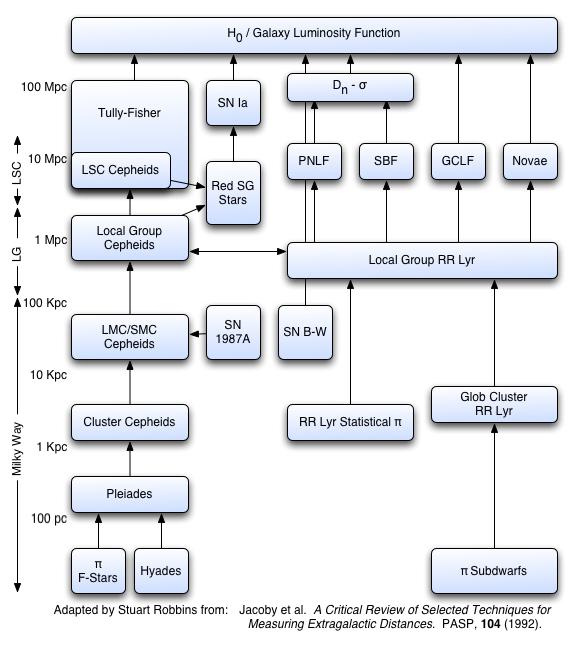
The Distance Scale Ladder
- Uncertainty propogation through the distance ladder: for small uncertainties,
- magnitude error ~ fractional luminosity error
- distance error ~ 0.5 * distance modulus error
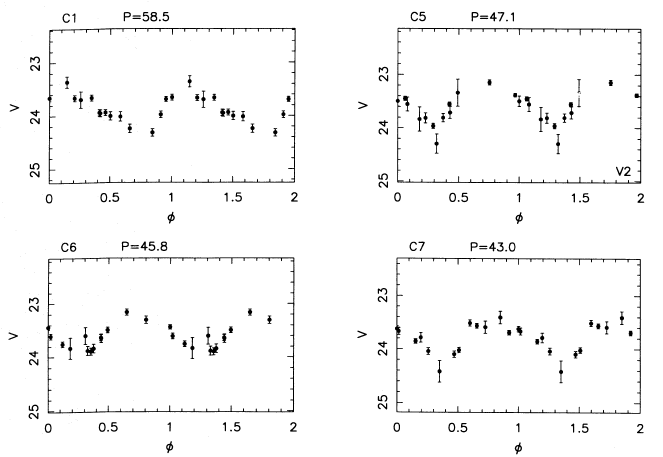
Cepheid Distances via Hubble (example: M101, of course!)
from Kelson etal 1997:
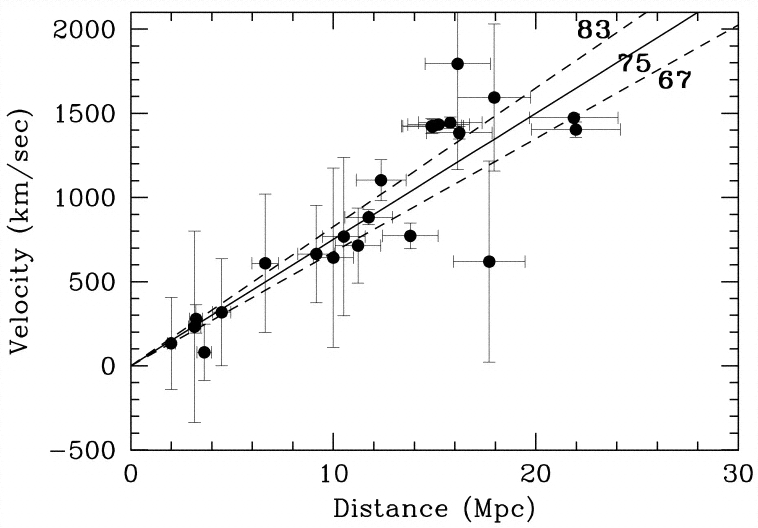
Cepheid (only) H0 Estimate
The purpose of the HST Cepheid Key Project was not to get H0 directly, but to improve calibration of other distance indicators!