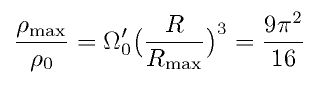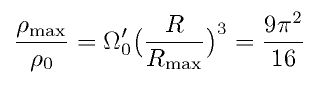We are going to look at the growth
of
structure in simulations with differing cosmological parameters. The
simulations are the "Hubble Volume Simulations" and more information
can be found at http://www.mpa-garching.mpg.de/Virgo/hubble.html.
I have grabbed the cluster catalogs from two simulations: LCDM and tauCDM.
A description of these files can be found here --
look under "Cluster Catalog Files". The cosmological parameters of the
sims are given by:
- LCDM: H0=70 km/s/Mpc, OM=0.3, OL=0.7
- tauCDM: H0=50 km/s/Mpc, OM=1.0, OL=0.0
Make a plot of the (log of the) comoving number density (logN in
#/Mpc^3) of clusters as a function of z (from z=0 to z=2) in the two
simulations, as well as the (log of the) ratio N(LCDM)/N(tauCDM) as a
function of
redshift. Describe why
the shapes of the plots look like they do.
Repeat the calculation just for the most massive clusters -- those with
velocity dispersions > 600 km/s. Comment on any differences you see
from the first plot.
You'll need to make use of astropy's cosmology routines for this, in
order to work out the comoving volume in each of your redshift bins.
You can get this by grabbing the total volume out to the edge of each
of your bins, then doing a np.diff to get the volume within the bin;
this shows how to do it for the LCDM cosmology:
from
astropy import cosmology
LCDM=cosmology.LambdaCDM(H0=70,
Om0=0.3, Ode0=0.7)
zbins=np.arange(0,2,dz) # THIS
SETS UP THE EDGES OF YOUR BINS (dz is your redshift binwidth)
bincenters = (zbins[:-1] +
zbins[1:]) / 2.0 # THIS CALCULATES THE CENTER OF THE BIN
dvol=LCDM.differential_comoving_volume(zbins).value
# THIS GETS VOL PER UNIT REDSHIFT PER UNIT SOLID ANGLE
dvol=4.*np.pi * dz * dvol # THIS
GETS THE TOTAL VOLUME WITHIN EACH BIN OF REDSHIFT
There is a "chunk of the Virgo
consortium universe" available for you here.
The data come from a massive simulation of a cube of the universe
measuring 140 Mpc on a side. Details of the simulation and the galaxy
creation can be found at http://www.mpa-garching.mpg.de/Virgo/data_download.html
The data give the x, y, and z coordinates in Mpc and star formation
rate in solar masses per year of 8384 simulated galaxies.
We are going to define subsets of galaxies as "late types" (ie Sb/Sc
spirals) and "early types" (ellipticals and S0's) based on their star
formation rates. Let's say late types are things with SFR's > 1
Msun/yr, and early types are things w/ SFR's < 0.1 Msun/yr. (Does
this definition make sense?)
- Plot up x vs y for all galaxies to give a feel for what the
data look like (remember to set the
aspect ratio properly on your plots!). Then do the same
thing just for E's and just for
S's. Describe any differences and explain whether or not it makes sense.
- Now
calculate the two point correlation function for all the
galaxies (see below for how to do this). Do this for seperations
between 1 and 10 Mpc, then fit a power law and derive the clustering
length, r0. How do your numbers compare to the numbers discussed in
class? Also describe qualitatively what this plot is telling you about
how galaxies are distributed.
- Now do the same thing just looking at 2 point correlation
function for spirals only, and again for ellipticals only. Plot them
up, fit power laws, and derive the clustering lengths. Describe the
differences you find in the clustering lengths for each sample. What
does this tell you about the clustering of different types of galaxies
in the universe, and does this make sense qualitatively based on what
you know about galaxies?
Calculating the 2ptCF: First, install astroml
if you haven't already (see below). Then to calculate the
2ptCF of a sample of N galaxies with x,y,z coordinates, do the
following:
from astroML.correlation import
two_point
pos=np.array([x,y,z]).T # YOU
WANT AN ARRAY WITH SHAPE (N,3), NOT (3,N)
rbins=np.arange(1,12,1) # BINS OF
SEPARATION (IN MPC)
rbincenters = (rbins[:-1] + rbins[1:]) / 2.0
corrfunc=two_point(pos,rbins)
Installing astroml:
In a jupyter notebook, Chris Carr reports that you should be able to simply say
- !python -m pip install --upgrade pip (if you need to update pip)
- !pip install astroml
If you don't use jupyter notebooks, you
can just do the same thing from the command line of a shell window,
just omit the exclamation points from the beginning of the lines.