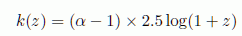ASTR/PHYS 328/428 HW #2
1. The K-correction
Quantitatively, the K correction is written as m-M = 5*log(dL) - 5 + K(z)
If you are observing through a filter that transmits from lambda1
to lambda2, the flux in the bandpass from a distant object
is given by
where Llambda is the luminosity per unit wavelength (measured in erg/s/cm2/Angstrom, for example), and te
refers to the spectrum we see in the galaxy at high redshift, ie at a time te.
With this in mind, show that the K-correction is given by
where t0 refers to observing the galaxy if it were in the local universe at the present time.
Helpful hint: Remember that the K-correction corrects for redshifting of the light -- the fact that compared to galaxies in the local universe we are seeing bluer light and a narrower bandpass when we observe galaxies at high redshift. So in terms of flux, we would correct the observed flux by multiplying that observed flux by the factor
X = flux[no-redshift-effects]/flux[observed],
and since the K correction iis in magnitudes (not linear flux units), the K correction will be given by -2.5log(X).
Now, if a galaxy emits a spectrum 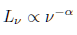 (where Lnu is the
luminosity per unit frequency) show that
(where Lnu is the
luminosity per unit frequency) show that 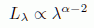 and that the k correction can be written simply as
and that the k correction can be written simply as
Helpful hint: Remember, regardless of whether we express things in terms of wavelength or frequency, if we have a filter with a wavelength width dlambda=lambda2-lambda1, it will have a frequency width dnu, and the total amount of energy we get through the filter doesnt care whether we are thinking in terms of wavelength or frequency. So Lnu times dnu = Llambda times dlambda.
Since quasars typically have a spectrum with alpha ~ 1, this gives
them a negligible k-correction! Explain why that is -- what does alpha ~ 1 mean in terms of color (qualitatively) and why does that suggest the k-correction will not change much with redshift?
2. Galaxy counts
- Using Figure 1 from Metcalfe et al 1996,
calculate the logarithmic slope (dlogN/dm) of the galaxy number count function over the
magnitude range mB=21-26 for the following:
- the observed number counts;
- no evolution models.
- evolution models for q0=0.5 and q0=0.05.
- Using this dataset of counts from
the Hubble Ultra Deep Field, create your own version of the
Metcalfe plot, and calculate the slope of the observed galaxy number
count function over that same magnitude range. Make sure to cut out
stars (objects with "stellarity" > 0.8 or so). Note that the UDF
covers
9 square arcmins of the sky.
- Discuss the comparison of your plot with that of Metcalfe etal,
in the following terms:
- overall match in the curve
- match of the slopes
- evidence for galaxy evolution
3. Hubble's Law vs Cosmological Distances
In the very local universe, we often will use Hubble's Law (v=H0d) to get distances to galaxies using their observed recession velocity. But we've seen in class that distances take on different definition on cosmological scales. So let's see how far out in redshift we can go using Hubble's Law before the errors introduced by ignoring cosmological effects become big. Let's assume we are observing a galaxy with an absolute magnitude of MV=-21 and a size of r=20 kpc. Adopt a cosmology of H0=72 km/s/Mpc, OmegaM=0.3, OmegaL=0.7 and make a plot of the following as a function of log(z) for log(z)=-2 to 0 (so z=0.01 to 1.0):
- A plot of the apparent magnitude of the galaxy as a function of log(z) under two cases: 1) using Hubble's Law and 2) using the correct cosmological luminosity distance. At what redshift does using Hubble's law introduce a magnitude error of 0.1 magnitudes? At what redshift is the magnitude wrong by 0.5 magnitudes?
- A plot of log(apparent size, in arcsec) versus log(z), again plotting both the Hubble's Law case and the proper cosmological case on the same plot. At what redshift does Hubble's law introduce a size error of 10%? At what redshift does Hubble's law introduce a size error of 50%?
- Finally, make a plot of observed surface brightness as a function of redshift in the two different cases. (Remember surface brightness in mag/arcsec^2 is defined as mu=m+2.5log(area[arcsec^2]) -- IT IS NOT magnitude divided by area!). At what redshift have cosmological effects dimmed the surface brightness by 0.5 mag/arcsec^2?
Again, if you need it, here is a data table giving luminosity distance (in Mpc) as a function of log(redshift) for the H0=72 km/s/Mpc, OmegaM=0.3, OmegaL=0.7 universe. But if you can, you really should be using astropy for this.
4. Descriptive Summary: Observing high redshift galaxies (1-2 typed pages of written description)
Explain how redshifting distorts our view of galaxies in the high redshift universe. Describe physically (but not mathematically-- I dont want equations!) how and why a star-forming spiral galaxy like the Milky Way would change in its optical appearance (and in our ability to detect it) if we could move it to higher and higher redshifts. If we did the same exercise with a massive elliptical galaxy what would happen and how would it be different from what happened with the spiral galaxy? Including sketches are fine, but they don't count towards the page limit.
Clarification on page limit and content: If you like writing your essays in single-spaced, close-packed text with narrow margins, one page may be sufficient. If you like double-spacing your text with margins you could drive a truck through, you'll probably want to be writing two pages of text. One page of double spaced text is probably not sufficient to give a through, clear, and complete description of all the effects that are impacting the appearance of high redshift galaxies. The important thing here is the quality of the scientific explanation, not the specific word count. If you are padding your essay with lots of flowery generic introductory material that doesn't contribute to the explanation, your essay is probably going to be incomplete even if you hit your page limts.
5. ASTR 428: Presentation Topic
Pick two possible presentation topics, and give me a one page written description for each. They should be focused on observational
cosmology and/or structure/galaxy
formation, and something that we aren't going to talk about in class.
I will look over your possibilities and recommend one for you to follow
up on.
Examples:
- Using the Lyman Alpha forest to constrain cosmology
- The Evolution of the Cosmic Star Formation Rate with Time
- Polarization of the CMB
- Cosmological applications of weak lensing
- etc
You will give a ~ 30 minute in-class
presentation on this topic during the last week of class.
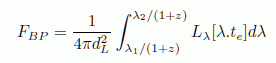
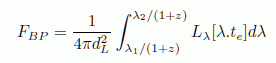
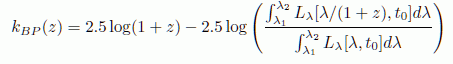
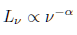 (where Lnu is the
luminosity per unit frequency) show that
(where Lnu is the
luminosity per unit frequency) show that 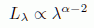 and that the k correction can be written simply as
and that the k correction can be written simply as