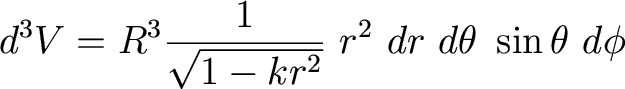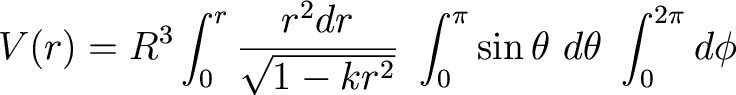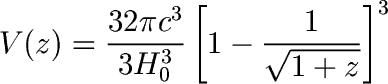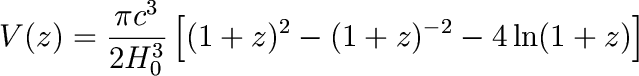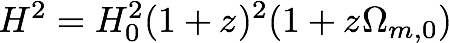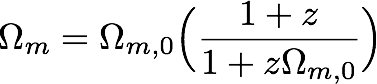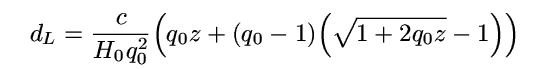Astr/Phys 328/428 Homework #1

---

1. Volume of the Universe

Step 1: Find the volume of the Universe out to a comoving distance r. Using the Robertson-Walker metric, we can define the differential volume element as

which means the volume out to a comoving distance r is given by

Solve to get an analytic expression for V(r) for k=-1,0,1.

Step 2: Find the relationship between comoving distance r (which you've calculated the volume for, but is unobservable) to redshift z (which is observable).

Start by using the R-W metric and integrating along the path of a light ray.  Do this exercise using a flat, matter dominated OmegaM=1 universe, remembering that R(t)~t^2/3 in such a universe. While this cosmology is certainly not the correct one, it is a useful "benchmark" to compare to (and it is analytically tractable!). This should give you a relationship like this: r=f(R,t0). Then use the Lemaitre equation and the expression for t0 to turn it into r=f(z,H0).

Step 3: Combine the relationship in steps 1 and 2 to show that

• V(z) is different in different universes. For example, using the same techniques, but with messier math, we can show that for an empty (i.e., non-Lambda, OmegaM=0) universe, the volume is

While for positively curved, OmegaM=2  universe we have

• On one figure, plot the volume (in Mpc³) out to a redshift z in each universe, from z=0 to z=3. Use H0=70 km/s/Mpc for these calculations and also overplot the volume in a LCDM universe with OmegaM=0.3 and OmegaL=0.7. The easiest way to do this is with the astropy.cosmology package, but for those who don't use astropy, here is a table of the volume (in Mpc³) as a function of redshift in such a universe.
  
• If the distribution of galaxies in the universe is completely homogeneous (meaning the number of galaxies per unit volume is a constant everywhere), plot on one plot the relative number of galaxies you see (per unit redshift) at a redshift z as a function of redshift in each of those four cases.
  
• If you could see all bright galaxies in the universe out to a redshift of z=2, what would the median redshift of the galaxies be in these four universes? Explain qualitatively why this makes sense.
  
• Why is this test (called the count-redshift test) a difficult test to perform? Think about observational issues, as well as the underlying physical assumptions behind the test.
  

2. The Flatness of the Universe

Starting with the Friedmann equantion for a Lambda=0 universe, show that the Hubble parameter can be written as:



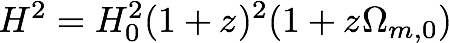
Helpful hints:

• First, rewrite H in terms of rho0 and z.
• Then rewrite rho0 in terms of Omega0 and H0.
• Then rewrite the Friedmann equation as it is at z=0.
• Then combine together what you get via those three hints to get the expression we want.

Then use that to show that



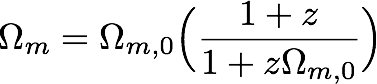
Helpful Hints:

• Start with writing Omega in terms of rho and H.
• Then substitute for H using the expression you derived in the first part of the problem, and also rewrite rho in terms of rho0 and z.
  

• At large redshifts (ie in the early universe), show that the Universe is essentially flat for any plausible choice of Omega_m0. Does this argument also hold for universes with a cosmological constant? Explain.
• Take your expression for Omega(z) and rewrite it so that you have an expression for Omega_m0 as a function of Omega(z) and z. Calculate what Omega_m0 would be if, at a redshift of z=1000, Omega had the value of 0.95, 1.000, or 1.001. What does this suggest about the value for Omega_m0?

3. Apparent Magnitudes and sizes of distant objects

In Lambda=0 universes, the "luminosity distance" (ie the distance measure you use when calculating brightnesses of objects) can be expressed analytically, and is given by


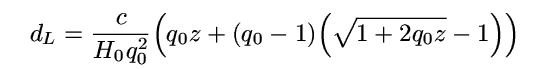The giant elliptical galaxy M87 has a V band luminosity of 10¹¹ L_sun and an effective radius of about 10 kiloparsecs. Imagine moving M87 to different redshifts, and plot its apparent V magnitude as a function of redshift from z=0.1 to z=2.0 for universes with q0=0.1, 0.5, and 1.5. Ignore K-corrections for this calculation, but describe qualitatively what the K-correction will do to your plot. Also, explain qualitatively how these universes differ in terms of their expansion history and spatial curvature.

Make a second plot showing the angular size of M87 (in arcseconds) as a function of redshift over that same redshift range.

For each of these different universes, answer the following:

• If you were constructing a sample of galaxies brighter than m_V=20, at what redshift would an M87-type galaxy no longer be included in your sample?
• If you were constructing a sample of galaxies with angular sizes greater than 1.5 arcsec, at what redshift would an M87-type galaxy no longer be included in your sample?

ASTR 428 additional question:

5. Lookback Times and Age Constraints

Use either the astropy cosmology package or the Cosmology Calculator for this exercise.

• It's 1990. You are a good, party-line cosmologist and "know" that OmegaM=1, and that there is no such thing as the cosmological constant. You also "know" that globular clusters are 14-16 Gyr old. What can you say about H0?
• A few years later, you decide that the measurements of H0 are getting better, so you need to believe them. So take H0=55, and tell me what constraint you can place on OmegaM. What about if you believe H0=65? H0=75?
• And then Hipparcos comes along (around 1997) and tell us that GCs are further away -- this means the ages of the globular clusters get revised downwards to 11-13 Gyr. Why does the further distance mean a younger age? At the same time, you decide, for better or worse, that you like H0=65. Now what constraints can you place on OmegaM?
• Later, in 1998 the high redshift galaxy LBD53W091 was discovered. It lives at a redshift of z=1.55, and its was determined to have a minimum age of 3.5 Gyr. How does this change your constraints on OmegaM?
• Six months later, the age of LBD53W091 was revised downwards, and became 1.7 +/- 0.3 Gyr. NOW how do your constraints on OmegaM change?
• Finally, this wacky Lambda idea starts to take off, so you have to consider OmegaL as well. Given your GC ages and H0, pick values of OmegaL and, for those values, place limits on OmegaM. Make a plot of your results on an OmegaL-OmegaM plane, showing regions of "allowed cosmology" given your GC age constraints.