The volume of space in the thin patch between
r and r+dr
is
![]()
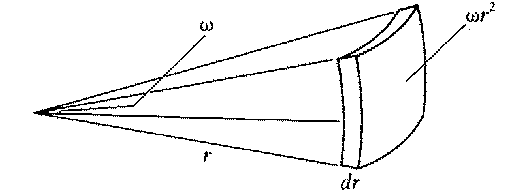
| Imagine looking at stars in a patch
of sky of
solid angle The volume of space in the thin patch between
r and r+dr
is
|
 |
|
If the galaxy has a uniform
density of stars
(given by n), and we integrate over radius, we get the total number of
stars between us and r:
|
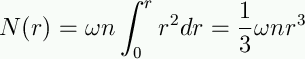 |
|
Now remember the relationship
between absolute
and apparent magnitude...
|
|
|
...which we can turn around to
solve for
r...
|
|
|
...and plug into N(r) to get N(m),
the number of stars brighter than some apparent magnitude m:
|
|
|
or:
|
So for every magnitude fainter we go, we ought to see 100.6 = 4 times as many stars. We don't.
But it gets worse. Let's look at how much light we'd
be
seeing from these stars.
|
Let's say the apparent
brightness of an
m=0 star is l0. Then, using the definition of magnitudes,
the
light coming from a star of apparent magnitude m is:
|
|
|
so the total amount of light
coming from
stars of magnitude m is:
|
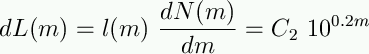 |
So the total amount of light coming from all stars brighter than apparent magnitude m is:
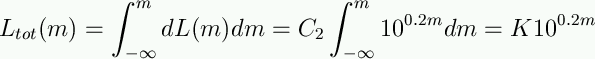
This diverges as m gets bigger: infinite brightness!
This problem is known as Olber's paradox. If the galaxy were infinite and homogeneous, the sky should be blazingly bright.
So what's the point of this failed exercise? It's
not
a failure! Turn the question around: fit star counts to different
models
of stellar distributions to derive the structure of the galaxy.