The Solar Motion
How do we define the motion of the Sun?
How would we know the Sun is moving at all?
Look at the velocities of stars around us.
- Most stars
have a small velocity relative to us, < ~ 30 km/s
- Metal poor halo
stars have a high relative velocity, ~ 200 - 250 km/s
What does this mean?
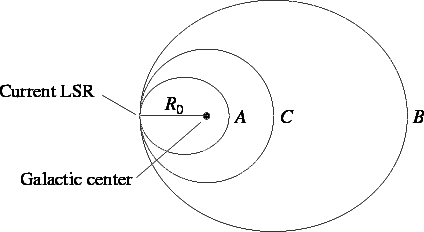
The Local Standard of Rest
Let's define a coordinate system:
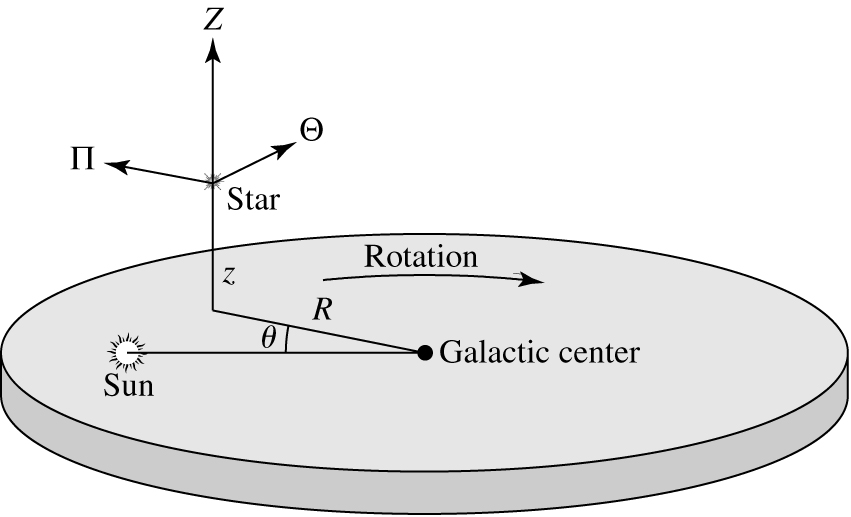
Position
|
Velocity
|
R = Radius (cylindrical)
theta = Angular coordinate
z = Distance from plane
|
Pi = velocity in/out from center
Theta = tangential velocity
Z = up/down velocity
|
Define a point in space that is moving on
a perfectly circular orbit around the center of the
galaxy at the Sun's galactocentric distance. We measure
all velocities of stars relative to this point, which is
known as the Local Standard of
Rest.
The velocity of the Local Standard of
Rest (LSR) is then given by
(Pi, Theta, Z)LSR = (0, Vcirc, 0)
Now we define the velocity of stars relative to the LSR.
(u,v,w) = (Pi, Theta-Vcirc, Z)
For
example, look at three hypothetical orbits:
- Star A lags the LSR -- negative tangential
velocity (v < 0)
- Star B leads the LSR -- positive tangential
velocity (v > 0)
- Star C orbits with the LSR -- circular orbit (v=0)
Note: The LSR is not the
orbit of the Sun!!!
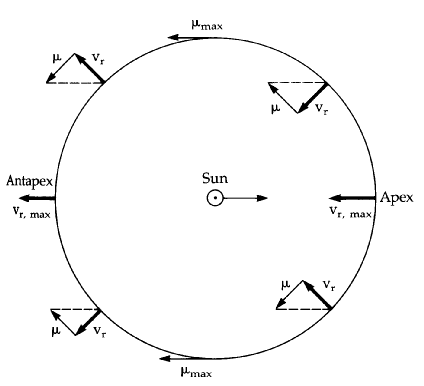
What is the Sun's motion relative to the LSR?
Look at all the disk stars
around us, and measure their radial velocities (vr) and
proper motions (mu). Do this for lots of stars, and take
the average along different lines of sight.
- If the sun wasn't moving, what would
you expect to see?
In fact, you should see that, on
average, star move towards us in one direction and away
from us in the opposite direction, due to the Sun's motion
relative to these nearby stars.
The residual non-zero averages give us the Sun's peculiar motion: (u,v,w) = (-10, 5,
7) km/s
The Sun is moving
- a bit towards the galactic center
- faster than the LSR
- northward out of the galactic plane
(Remember this is after we've factored out the
general rotation velocity of the disk!)
|
 |