Parallax Distances

Stick your thumb up at arm's length. Close one eye, then the other (and open the first one, so you can still see...). See how your thumb's position shifts relative to the background wall? This is called parallax. Now bring your thumb closer to your face, and do it again. The shift is bigger! You can use parallax to measure distance.
 

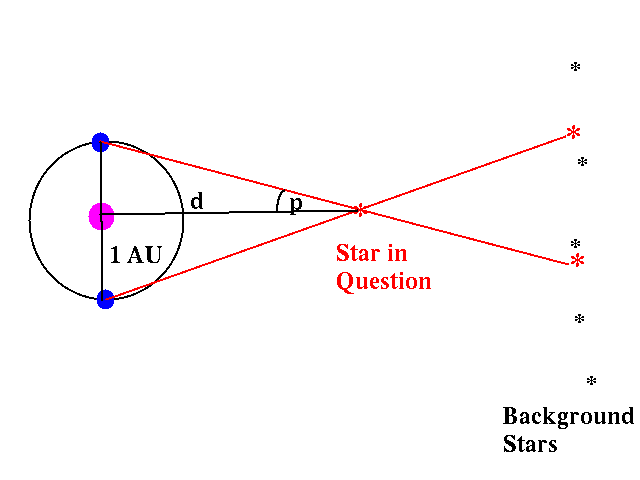
Okay, so let's do this with stars.

Instead of closing one eye and then the other, we observe a star six months apart, so that we are on opposite sides of the sun for each observation. Watch the star shift against background star field, and measure that shift.


Parallax Demo Animations (courtesy Erik Tollerud and James Davenport):


Define the parallax angle as half the observed shift:

Using trigonometry, we can solve for the distance. If we measure p in radians, we have:

(Why?)

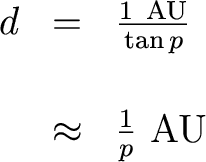
But we usually measure angles in arcseconds. Since 1 radian = 57.3o = 206265", we have

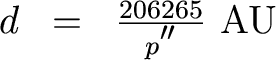
Okay, now comes the thinking part. Let's define a unit of measure called the parsec (pc) which is simply 1 pc = 206265 AU.  Then we have

 
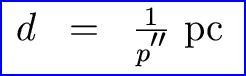
By definition, a parsec is the distance to a star which has a parallax angle of 1"
 

1 parsec is 3.26 light years. The nearest star has a distance of 4.2 light years, which is 1.3 pc. Its parallax angle is 0.77" -- small!

 

Stars are so distant that measuring parallax is difficult. Satellite measurements:


 Hipparcos
 Gaia
Dates
 1989-1993
 2014-2019
Limiting magnitude
 ~12
 ~ 20
Parallax precision
 milliarcsec 20 microarcsec (@ 15 mag)
200 microarcsec (@ 20 mag)
Distance
 < 1 kpc
 10 kpc
N(stars)
 ~ 105
 ~ 2x107 (1% accuracy)
~ 2x108 (10% accuracy)
Velocities
 no
 yes -- radial and space motions!