Disk Galaxies: Surface Brightness and Color
Luminosity Profiles and Surface Brightness
Unlike stars, galaxies are not point sources; their light is
distributed over a patch of sky with a given angular size. So we
describe their light distribution in surface brightness, which describes flux
per unit angular area on the sky. And just as flux can be measured in magnitudes,
surface brightness can be measured in magnitudes per square arcsecond.
In other words, if magnitudes work like this:
m = -2.5log(f) + c
where m is magnitude, f is flux, and c is a zeropoint, then surface brightnesses work like this:
mu = -2.5log(f/area) + c
where area is the angular area of the galaxy, and mu is a surface
brightness measured in magnitudes per square arcseconds. Think of it as
describing the total apparent magnitude of the light that is contained
in a box one arcsecond on a side.
VERY IMPORTANT: you cannot
multiply surface brightness by area to
get a total magnitude, just like you can't multiply magnitudes. The
relationship between total magnitude, surface brightness, and area can
be worked out as follows:
if
mu = -2.5log(f/area) + c, then
mu = -2.5log(f) + 2.5log(area) + c, so
mu = m + 2.5log(area)
Exponential disks
|
As with the Milky Way, the surface
brightness (flux per unit area) of spiral disks is described
by an exponential law: |
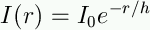 |
|
| Or, if we convert this to magnitudes
per square arcsecond: |
 |
Note that while the observed brightnesses and sizes
of
galaxies drop at larger distances, surface
brightness does not change. Look at a patch of the galaxy of fixed angular size, and imagine moving the galaxy to larger distance.
- The flux per stars drops as ~ r-2 (i.e., the inverse square law of light)
- The physical size of the patch gets bigger as ~ r, so its physical area goes as r2.
-
So each star is fainter by r-2 but the total number of stars in the patch increases as r2, so the flux coming from that patch = r-2 x r2 = constant.
The surface brightness of a galaxy is set by the density of stars inside it -- it is an intrinsic property of the galaxy,.
So we can measure the surface brightness of spiral
galaxies and learn immediately the luminosity density -- the density of starlight in Lsun/pc2 -- inside the galaxy without knowing the distance. Very useful! In the B filter, mu = 27 mag/arcsec2 corresponds to 1 Lsun/pc2. A galaxy with a surface brightness of muB = 22 mag/arcsec2 (5 mags brighter) has a luminosity density of 100 Lsun/pc2.
Galaxies show a wide range
in
central surface brightnesses; there is no preferred central
surface brightness. On the left is M101, a high surface brightness
galaxy;
on the right is Malin 1, a low surface brightness galaxy.
M101

|
Malin 1

|
Colors and color gradients
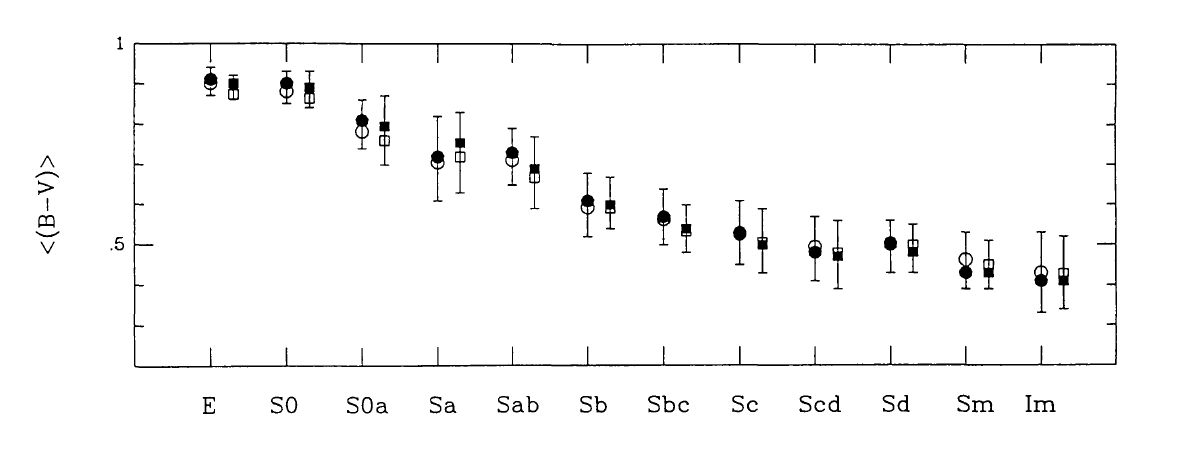
The colors of spiral galaxies are affected by stellar populations
-- the mix of young and old stars -- as well as dust. We saw that
spiral galaxies are bluer than ellipticals, and that their colors also
show a systematic trend with Hubble type: "Early" type spirals (Sa) are
redder than "late" type spirals (Sc).
But in general, spirals also tend to show color gradients
internally, where the outskirts are bluer than the inner regions.
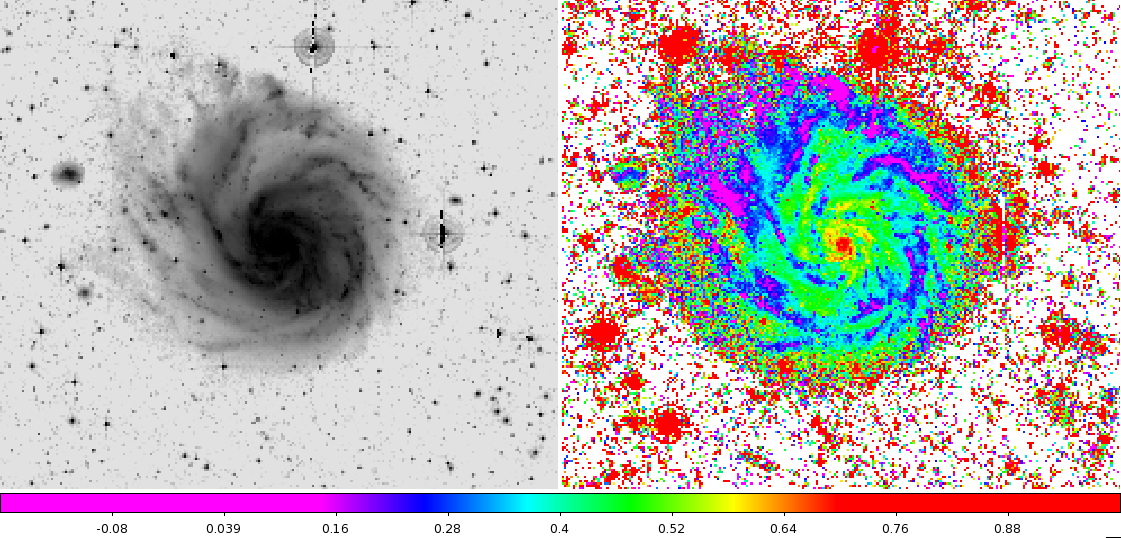
Example: M101 (from Mihos et al 2013):
And quantitative profiles of other disks from de Jong (1996). (Remember, color values are defined such that bigger numbers are redder colors....)
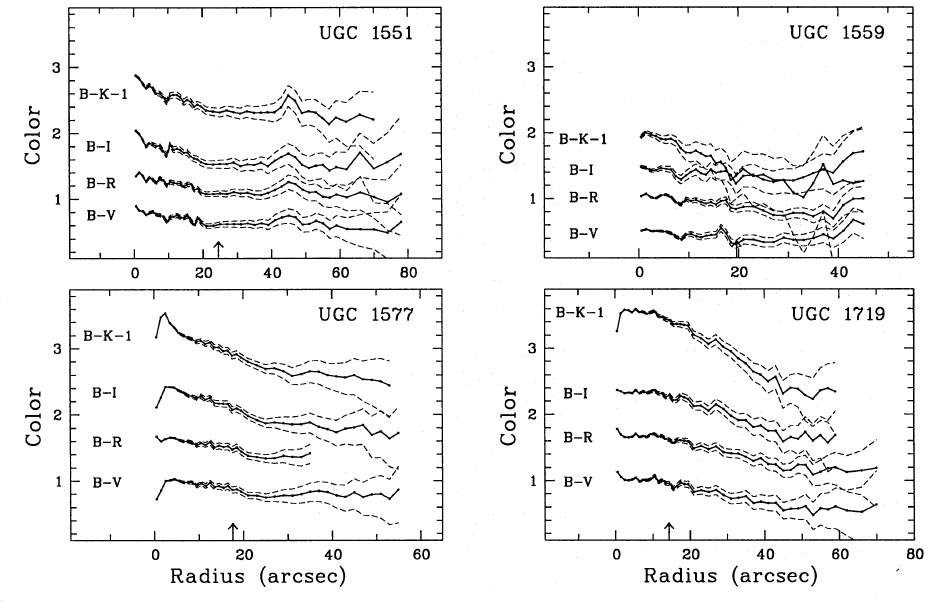
So the outskirts of disk galaxies tend to be younger (and probably
also less dusty) than the inner regions. This has led to the concept of
"inside out" galaxy formation models, where the inner regions of
galaxies form most of their stars early and the outer regions form stars more gradually over time.
How long can galaxies sustain star formation and keep building up their
stellar mass? Typical star formation rates in big spirals are a few
Msun/yr, and these galaxies typically have a few x 109 Msun
of interstellar gas. So their gas depletion timescales are thus a few
billion years, give or take, unless they can accrete gas from their
surroundings.....