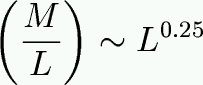Kinematics of Ellipticals

Remember how we characterize velocity of populations of stars.

rotation (v): the net rotational velocity of a group of stars
dispersion (sigma): the characteristic random velocity of stars

In the disk of our galaxy, v=220 km/s, sigma=30 km/s, so v/sigma ~ 7. This is called a cold disk.

Elliptical galaxies have much higher velocity dispersions, 100s of km/s. These are kinematically hot systems. v/sigma ranges (roughly) from 0 to 1.

Would you expect flattened ellipticals to have higher or lower values of v/sigma? Why?

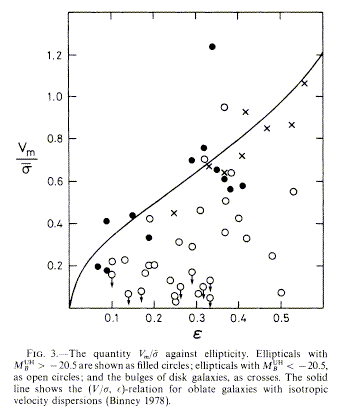
v/sigma actually correlates with luminosity.

Lower luminosity ellipticals have higher v/sigma -- rotationally supported.
Higher luminosity ellipticals have lower v/sigma -- pressure supported. Stars have different characteristic speeds along different axes.

The figure to the right shows v/sigma plotted against ellipticity (epsilon). The line shows expected shape for rotationally supported galaxies. (from Davies et al 1983)

The Faber-Jackson law

Remember the Tully-Fisher law for disk galaxies: L ~ v⁴. Can we make a similar law for elliptical galaxies using luminosity and velocity dispersion?

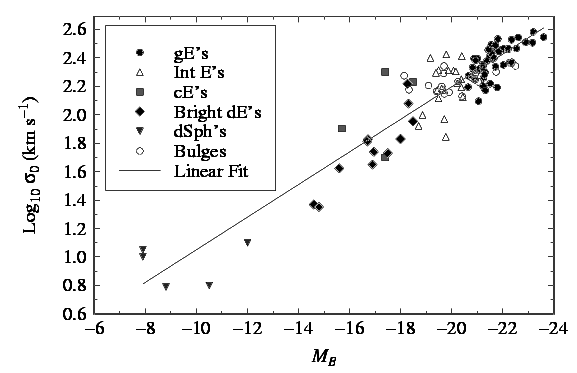
The Faber-Jackson law has a lot of scatter: at a given velocity dispersion, there is a range of +/- 2 magnitudes in luminosity. Compare this to the Tully-Fisher relationship, where at a given circular velocity, there is a range of a few tenths of a magnitude in luminosity.

Clearly, there is something messing with the relationship -- a second parameter.

The Fundamental Plane

In 1987, two teams of astronomers identified the second parameter -- the effective radius. Rather than two parameters correlating (in which case you fit a line), there are three parameters correlating (in which case you fit a plane).

We have 4 things we can measure:

Luminosity (L)
Effective radius (r_e)
Mean surface brightness (<I_e>)
Velocity dispersion (sigma)

There are only three independant variables here (L, r_e, and <I_e> are not all independant).

If you plot one versus another, the third introduces scatter, for example:

Surface brightness versus luminosity
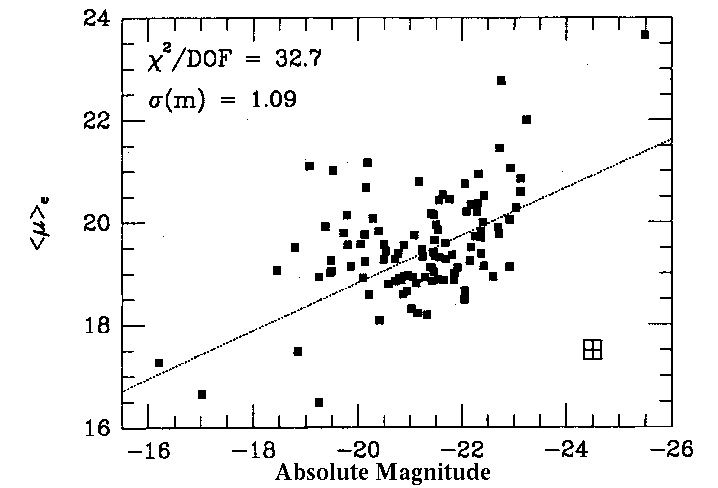
Velocity dispersion versus effective radius

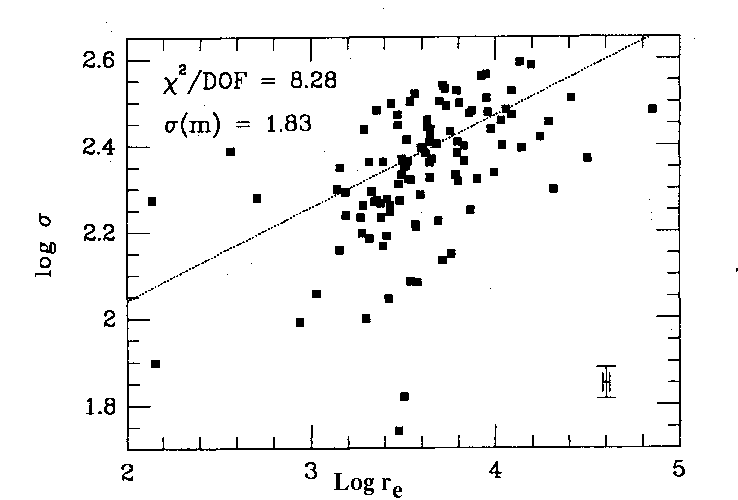
But if you plot one versus a combination of the other two, you can see a very tight correlation:

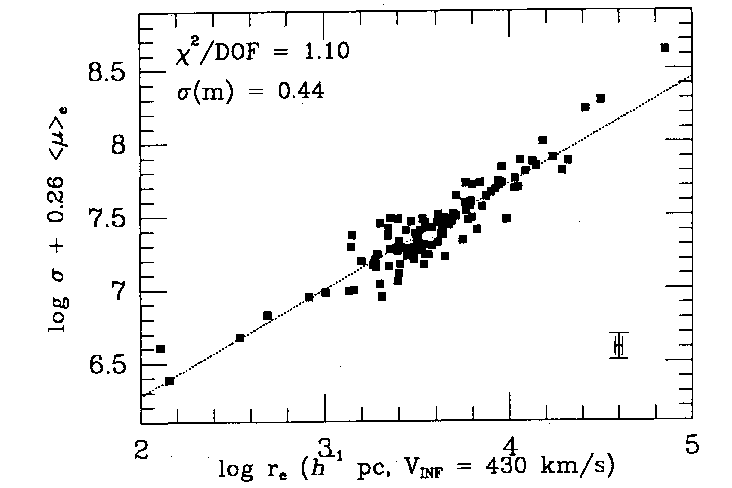
This correlated plane is now referred to as the fundamental plane. Since we have four observables, only three of which are independent, there are different representations of the FP which are all expressing the same thing. Here is another one:

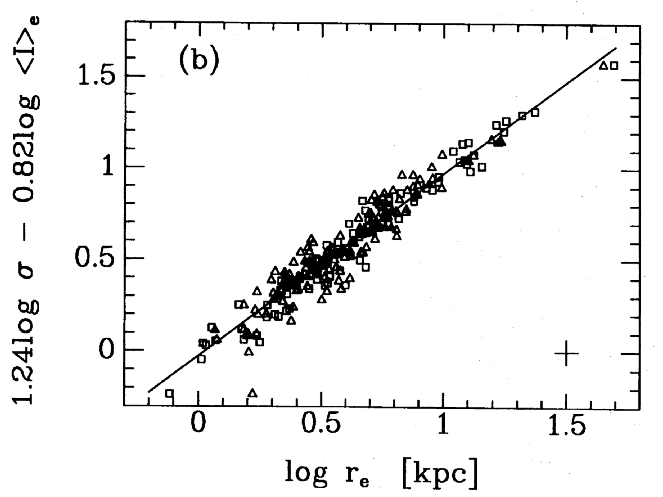
Or in other words

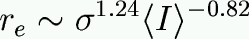
Examples of uses of the Fundamental Plane:

Distance Measuring: In the FP, r_e is measured in physical units: kpc. So if you know the velocity dispersion and effective surface brightness (both of which are distance independent measures), you can use the FP to work out the physical size of the galaxy. If you also measure its angular size, you can use trigonometry to solve for the distance to the galaxy.

Studying Galaxy Structure and Evolution: You can use simple algebra to show that one implication of the fundamental plane is that total (not stellar) mass-to-light ratio depends on galaxy luminosity:

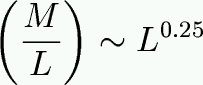
Why would this be? Whatever model we come up with to explain the formation and evolution of galaxies must also explain why more luminous galaxies have higher total mass-to-light ratios.

Central black holes in ellipticals

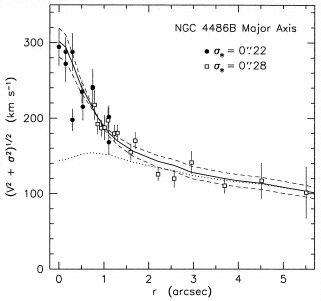
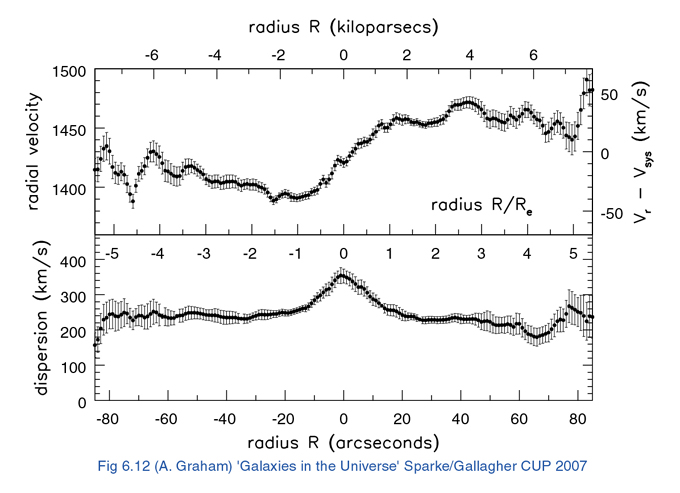
Stellar kinematics in the cores of nearby ellipticals show a rise in the central velocity dispersion. The stars are moving too fast for their gravitational potential -- some "dark mass" must be there.

(Kormendy et al 1997)

We can work out the "demographics" of black holes this way and study their connection to their host galaxies (courtesy Kormendy):

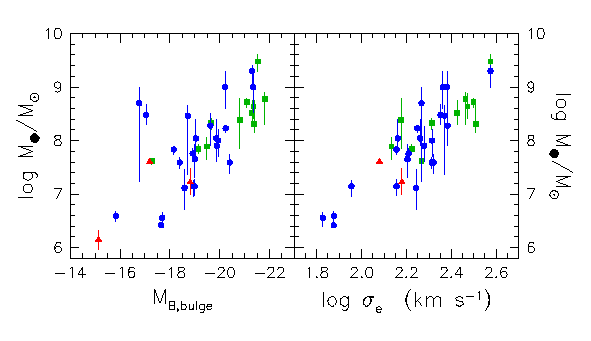
Plotted on the left is the black hole mass vs the absolute magnitude of the "bulge" of a galaxy, where in this case "bulge" refers to any spheroidal part of a galaxy -- ie, for a spiral galaxy it is the stellar bulge, while for an elliptical galaxy it is the entire galaxy. The implication here is that the black hole mass is about 0.1% of the bulge mass of a galaxy.

Plotted on the right is the black hole mass vs the velocity dispersion of the galaxy.