Observing objects in the High Redshift Universe

Mathematical details will be left to ASTR 328....

Cosmological Effects on brightness and size


When observing objects at high redshift, simple Euclidian geometry no longer works. We have to take into account the shape and expansion history of the universe, which various in different cosmologies, i.e., as a function of H0, OmegaM, and OmegaL. This means we have to know the cosmology to derive physical properties, or conversely, if we know physical properties we can infer the cosmological parameters.


So how do we measure luminosity, angular size, and surface brightness at cosmological distances? DON'T SIMPLY USE HUBBLE'S LAW!

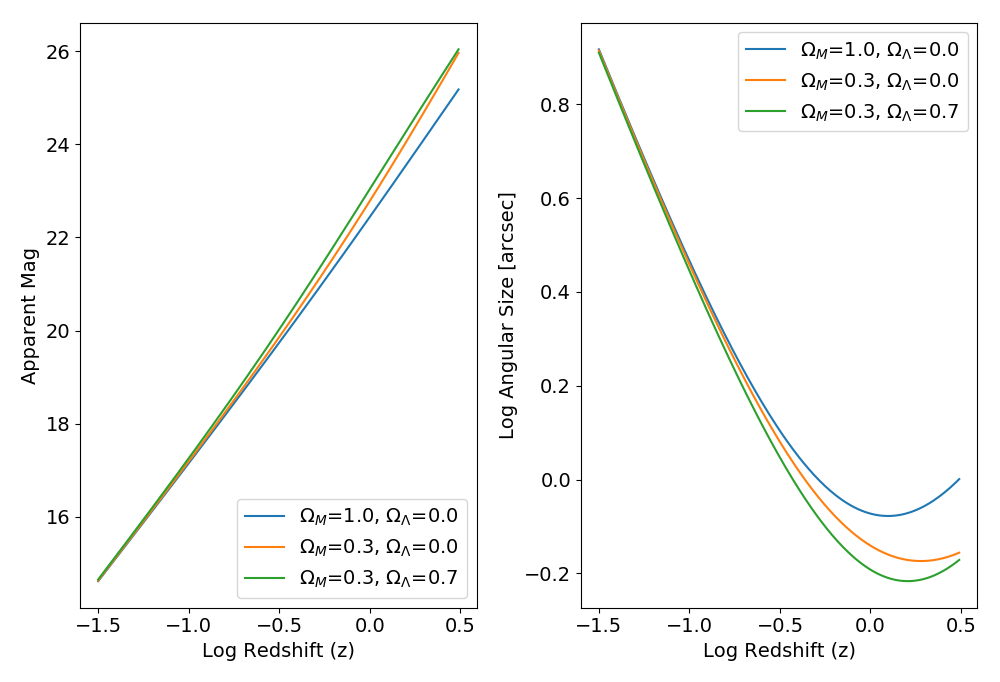
Luminosity distance

Normally, flux = Luminosity/(4piD2). But what do we mean by D in curved space? Let's define a luminosity distance dL so that we can simply use the normal flux equation, and then work out what dL is in different cosmologies.

First, define a coordinate distance that depends on the scale factor R and the comoving distance r. The energy flux you get from an object at that position is:
  • reduced because of normal inverse square law of light: f ~ L/4pi(Rr)2
  • reduced again becase the photons are being redshift and therefore reduced in energy: f ~ 1/(1+z)
  • reduced yet again because photons arrive more slowly due to cosmological time dilation: f ~ 1/(1+z)
Put them all together and note that we are observing at t=now, so R=1, and we get f ~ L/(4 pi r2 (1+z)2 ). So we can define dL = r(1+z), and solve for r (the comoving distance) as a function of z for different cosmological parameters. 		Angular size distance

Normally, the angular size of an object is given by theta=size/distance (using the small angle approximation). Under cosmology, we write

theta = size/(Rr) and then note that R = 1/(1+z), so

theta = size(1+z)/r

If we define the angular size distance as dA=r/(1+z), then we can use

theta = size / dA

like usual. 

With things defined this way, for any cosmology, the relationship between angular size distance and luminsosity distance is given by: dA = dL / (1+z)2

Note the huge difference as a function of redshift: a factor of four at z=1.....


Example: let's imagine looking at a big bright galaxy with effective radius of 5 kpc and absolute magnitude M=-21. How would it look at different redshifts in different cosmologies?





Surface brightness

Notice that things get fainter and fainter and high redshift, but their angular size behaves differently -- so surface bightness will change with redshift!

Since observed surface brightness is flux/(angular size)2, we can combine the two expressions above:

surface brightness =  flux/area ~ f/theta2 ~ (L/size2)(1+z)-4

for any cosmology.

So surface brightness drops as redshift increases. At z=2, surface brightness is down by 3-4 = 1/81 = 4.8 mag/arcsec2.



Instrumental complications: Filters and bandshifting

The above discussion about apparent brightnesses and the luminosity distance assumes you are detecting all the flux at all wavelengths -- i.e, measuring the bolometric flux. We never do this. We measure brightness over a range of wavelengths, ie through a filter. In terms of wavelengths, redshift both shifts and stretches light we see from distant objects. How does this complicate things?

  1. Redshift shifts the emitted spectrum we observe.

  2. Redshift stretches the emitted spectrum we observe. 
Example: if we are observing galaxies using the V filter, what part of its spectrum are we seeing?


at z=0
at z=2
central wavelength (Angstroms)
5500
1833
bandpass (Angstroms)
1000
333

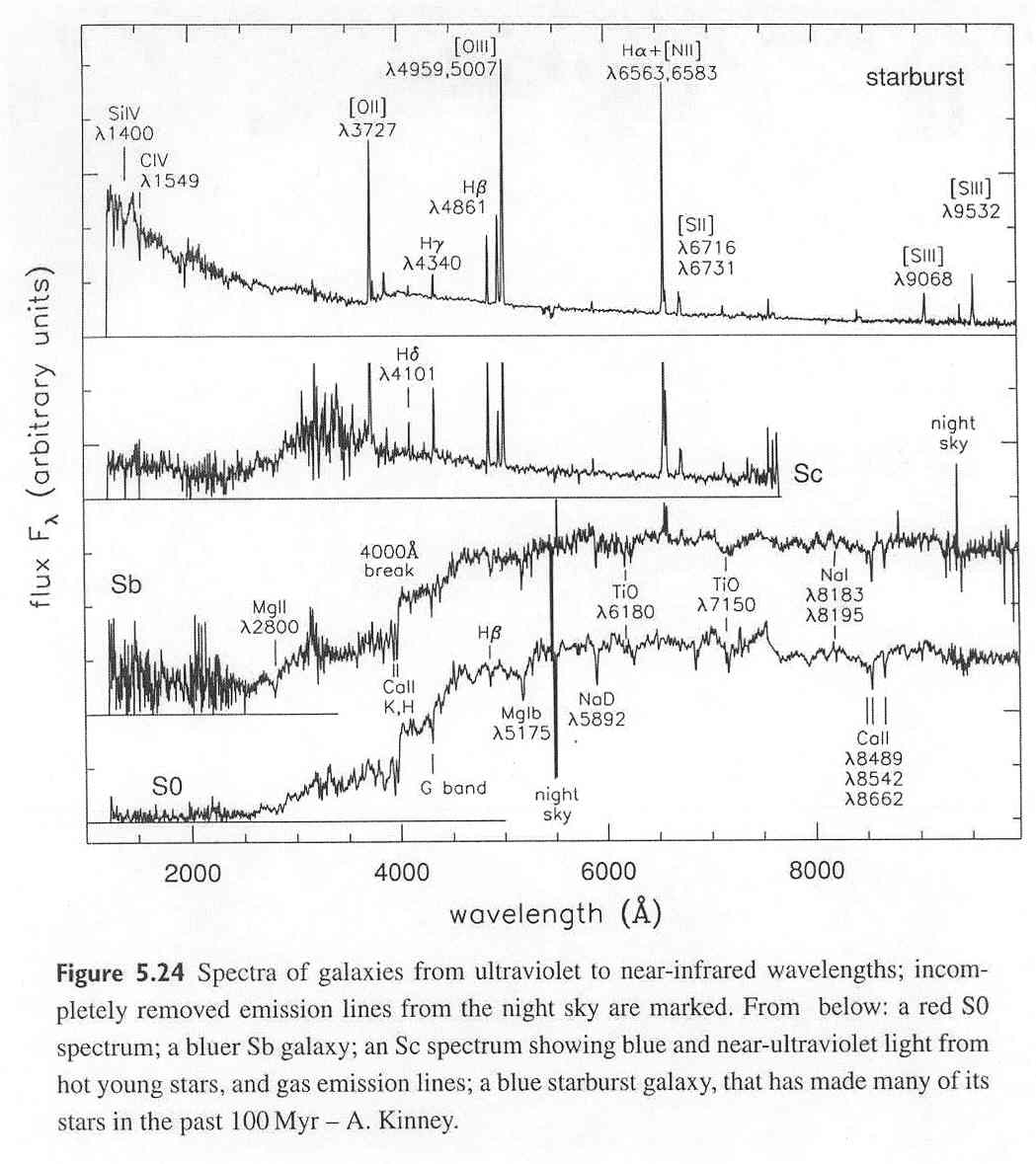
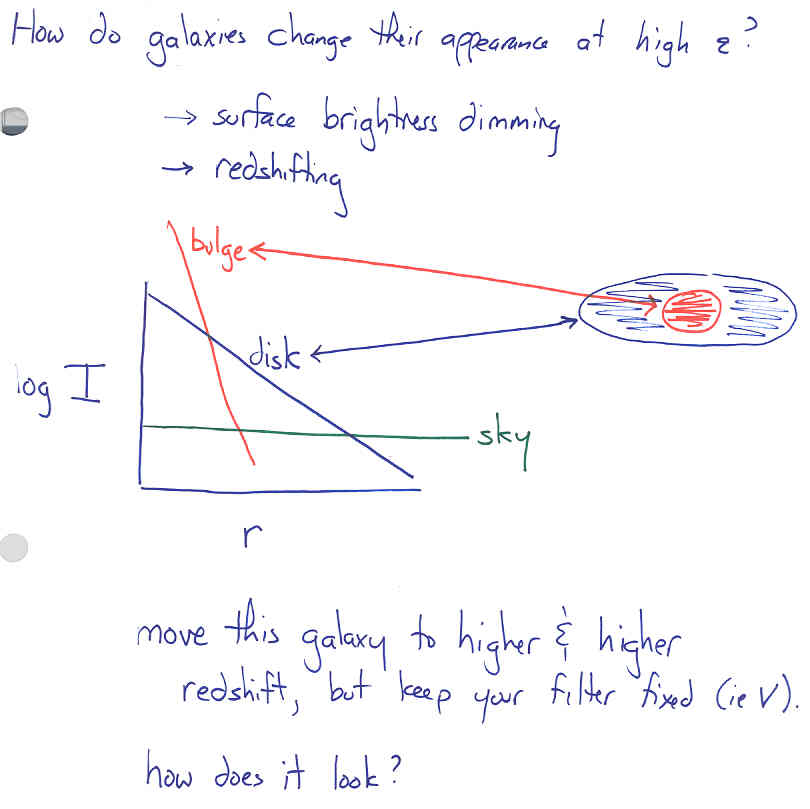
So when we observe high redshift objects, we are seeing them at intrinsically different (bluer) wavelengths. Things will look different!

Or, you can observe in redder (infrared) filters as you look at objects at higher reshift.





Appearance of high redshift galaxies


Put cosmology and bandshifting together and what do you get? Consider the luminosity profile of a spiral galaxy:




Galaxy Evolution


Finally, how would galaxy evolution change things -- what did today's spiral galaxies look like when they were young? What about giant elliptical galaxies like M87?