Using Supernovae to Study Cosmology

The Redshift-Distance Test

As a function of redshift, the apparent magnitude of distant objects changes under different cosmologies, for two reasons:

The shape of space determines how photons spread out as they move outwards (the classic 1/d² effect)
The expansion history determines how the photons are redshifted.

This can be worked out under different cosmologies to derive a form akin to our regular magnitude-distance expression:

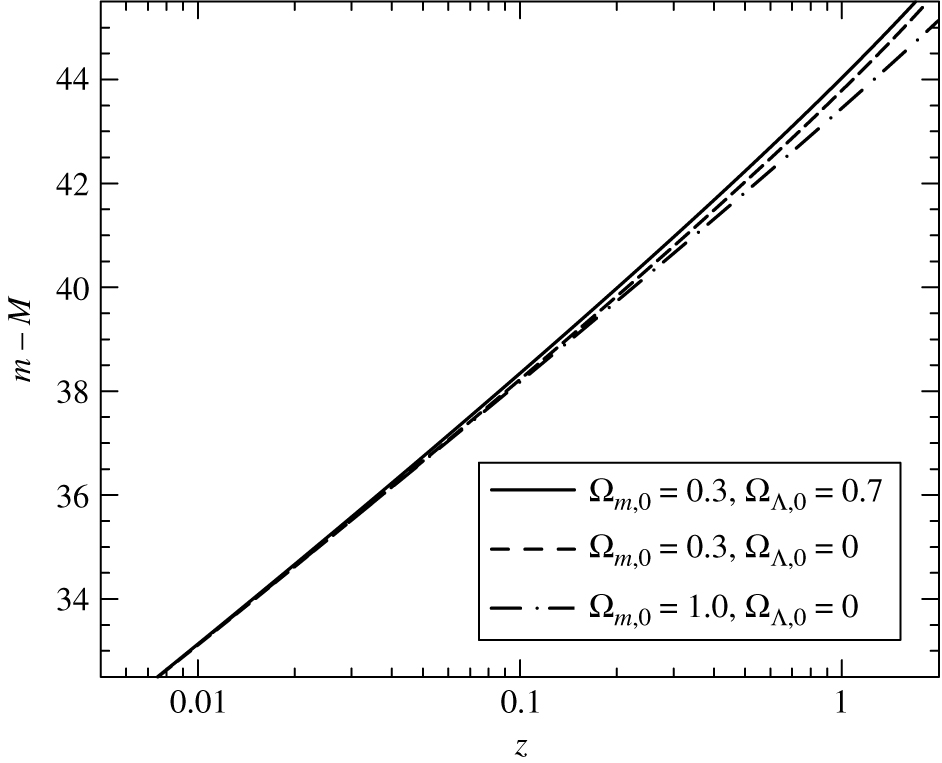
m-M = 5logd_L(z) -5

where d_L(z) is the luminosity distance, and depends on H₀, Omega_M, Omega_L, and k. We typically plot this using the distance modulus, not the distance, though (from Carroll and Ostlie):

If we had an object of fixed brightness -- a standard candle -- we could plot its apparent magnitude as a function of distance and work out the cosmology.

Remember Type Ia supernovae: the explosion of a ~ 1.4 Msun white dwarf. These are pretty good approximations to a standard candle, and they are extremely bright. That's exactly what we want to use for the redshift-distance test.

But are SN Ia's really standard candles?

Type Ia supernovae in galaxies w/ Cepheid distances (From Riess etal 2016):

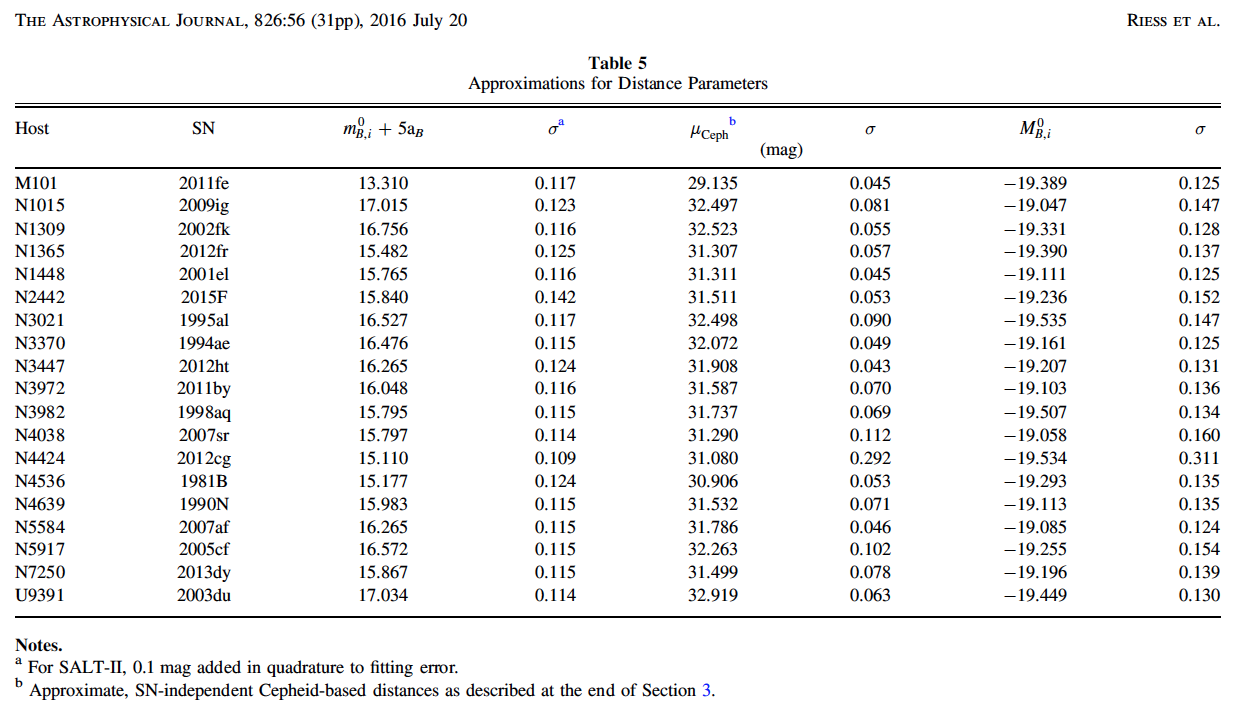
Which gives an average peak absolute magnitude of -19.26 +/- 0.16.

This uncertainty in peak mag includes the distance uncertainties to the galaxies, so the real dispersion in peak magnitude is even smaller, about 0.1 mags or so. That's a pretty good standard candle.

But there's a significant drawback to using Type Ia SNe. You gotta find them...

Using supernovae to study cosmology

Take a BIG picture of the sky.
Come back next month and take the same picture.
Compare the two. Differences?
If you find a possible supernova, take a spectrum of it and make sure it is a Type Ia SNe.
Also take a spectrum of the galaxy it lives in, to find its redshift.
Watch the supernova as it fades, so we can get its peak apparent magnitude. This is important -- you probably didn't catch it when it was at its peak, so we need to fit it to a standard light curve to derive its peak magnitude.
Keep doing this so you have a big sample of high redshift supernovae. Then compare those supernovae to ones at lower redshift.

Some plots, courtesy of the supernovae cosmology project at LBL and the high z supernova search team at CfA:

Example of a high-z supernova discovery

SNe + Host galaxies with HST

Redshift Magnitude Plot

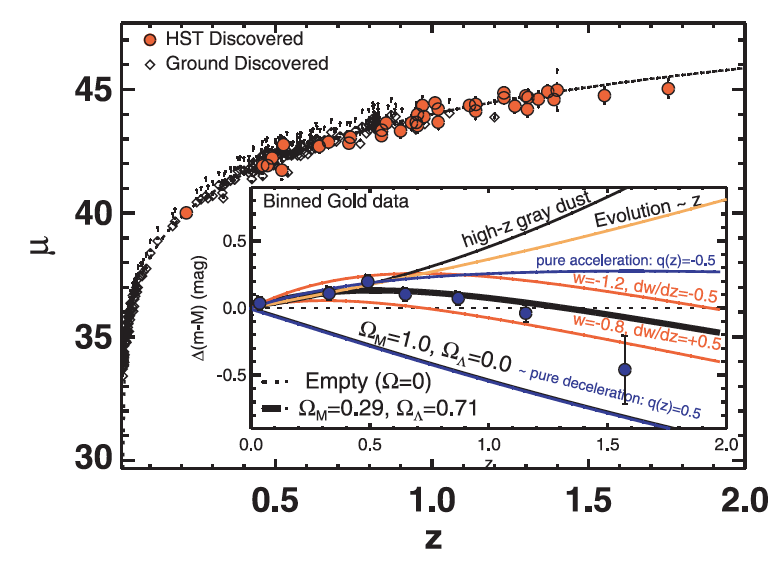
More recent data: HST discovered supernovae, extending to higher redshift (Riess et al 2007). In this plot mu=m-M, the distance modulus. Curvature in the data is inconsistent with models that use dust or evolution to explain faintness of high-z SNe; instead it is indicative of the "jerk" in the expansion history when lambda began to dominate and the universe went from decelerating to accelerating.