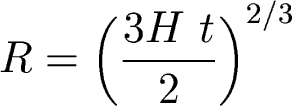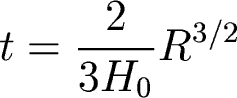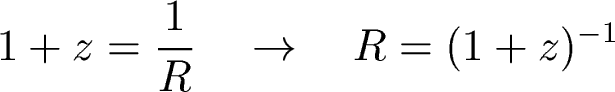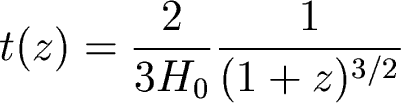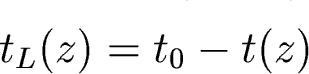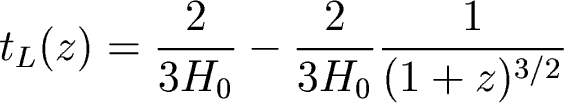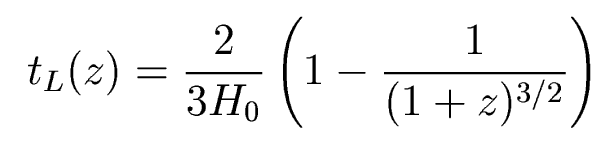Cosmological Times
One thing that comes out of all the different models is
the
age of the Universe, t0. t0 depends on H0,
OmegaM, and Lambda, so we can't uniquely determine cosmology
just from measuring the age of the Universe. But we can place
constraints.
How?
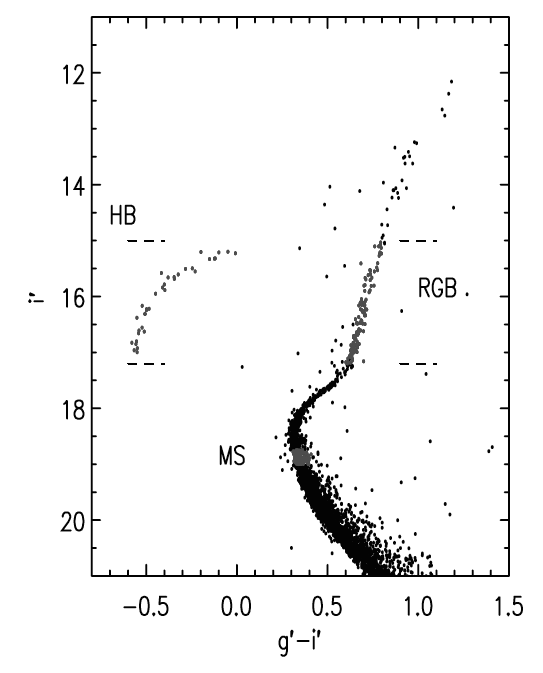
The Ages of Globular Clusters
Obviously, globular clusters can't be older
than
the Universe. We measure the age of a globular cluster by measuring the
main sequence turnoff in the color-magnitude diagram of GCs:
By measuring the luminosity and color of the turnoff,
and
comparing to models of stellar evolution, we can determine the ages of
the globular clusters. For M92 above, we get an age of ~ 11 Gyr (di Cecco et al 2010).
Typical numbers are 10-14 Gyr, with uncertainties ~ +/- 2 Gyr.
Ages of Lambda=0 Universes
| |
H0
|
OmegaM
|
t0 (Gyr)
|
|
A
|
72
|
1
|
9.0
|
|
B
|
40
|
1
|
16.3
|
|
C
|
72
|
0.3
|
11.0
|
|
D
|
72
|
0.1
|
12.2
|
|
E
|
85
|
0.1
|
10.3
|
We can see from this table that some models are
"ruled
out":
-
it's extremely hard to envision an OmegaM=1
universe.
-
it's extremely hard to envision a high H0
universe
(ie H0 > 80)
The Cosmological Constant
may be real
Ages of H0=72 Universes
| |
OmegaM
|
OmegaLambda
|
t0 (Gyr)
|
|
A
|
1
|
0
|
9.0
|
|
B
|
0.3
|
0
|
11.0
|
|
C
|
0.3
|
0.7
|
13.0
|
|
D
|
0.1
|
0.9
|
17.3
|
The Ages of High Redshift Objects
When we look at distant objects, we are seeing the
young
universe. How old are objects in a young universe? If we measure an
object
that is 3 Gyr old at a time when the Universe was only 2 Gyr old,
that's
bad...
Now we need to introduce a few concepts. When we
look
at an object at a given redshift, we can define (in
a model-dependent way):
-
Lookback time tL(z):
How far back in time we are looking.
-
Cosmic age t(z):
the
age of the universe at that redshift
Let's calculate this for one model: OmegaM=1, Lambda=0
For this model, we had (from last time) an expression
for how scale factor grows with time:
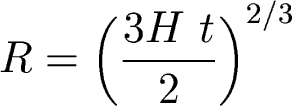
from this we solve for t:
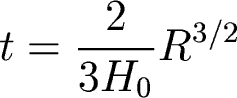
We also know how scale factor and redshift are
related:
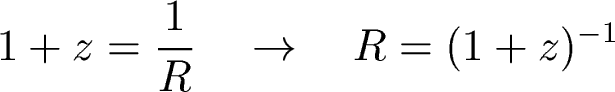
Plugging in, we get
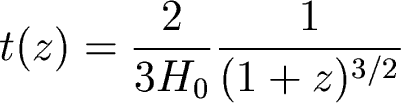
so the way we have defined things, lookback time can
be calculated this way:
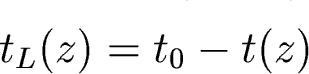
so
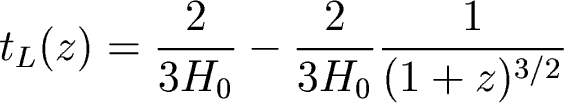
or
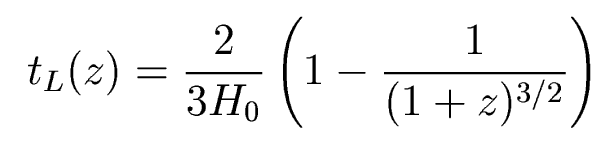
analagous but messier equations exist for other
cosmologies
as well.
So we can plot lookback time and age as a function of the observable, redshift for any cosmology.
Here it is for H0=72 universes with no cosmological constant:
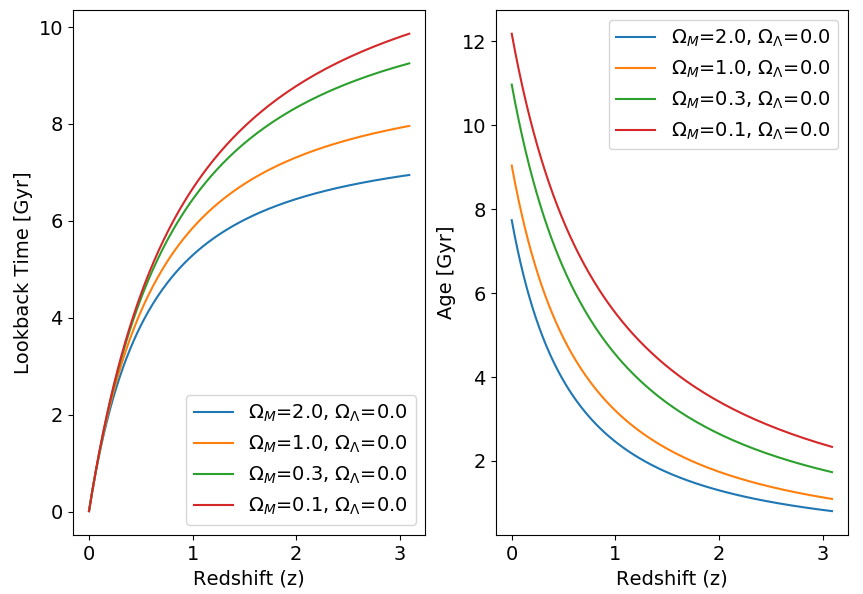
And here it is for spatially flat H0=72 universes with different mixes of matter and lambda:
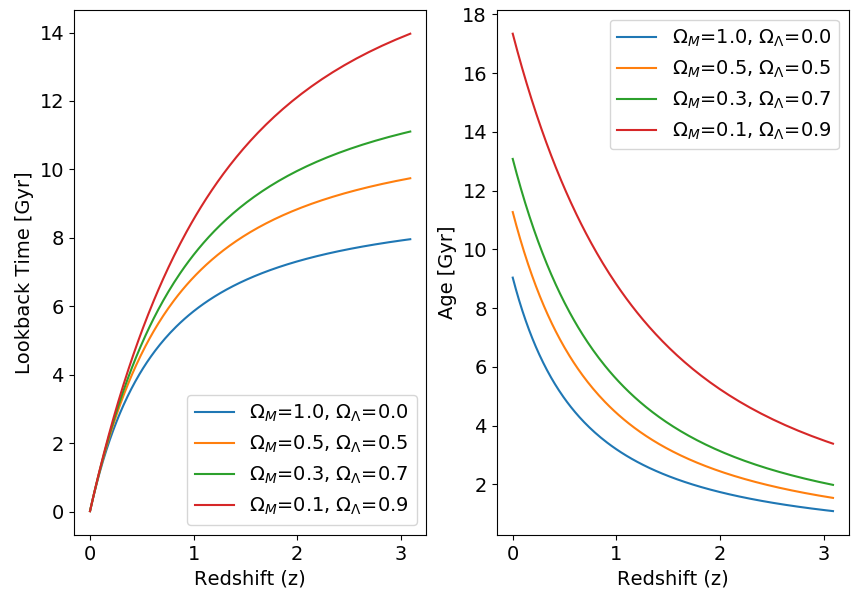
And remember, I can always shorten (lengthen) the
ages by using a larger (smaller) Hubble constant. But then I run into
the problem of being in conflict with the measured value of the Hubble
constant (H0=65-75 km/s/Mpc or so....).
So if we find an object of a given age at a given
redshift, that gives us a LOWER LIMIT on the age of the universe, and
this allows us to rule out certain cosmologies. For example globular
clusters today (z=0) give a lower limit on the age of the universe of
10-14 Gyr or so.
A while back, an elliptical galaxy was found at high
redshift
(z ~ 1.5) which looked to be at least 3.5 billion years old. How can
this
constrain cosmology? You tell me....