The Age of the Universe: first attempt

---

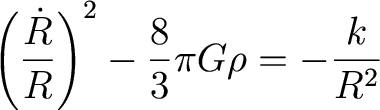
For many years, theoretical cosmologists believed that the most likely universe was a flat (or "critical"), matter dominated universe. Let's work out the age of that universe.

We had from last time, the Friedman equation, the dynamical equation that governs the expansion of the Universe. Let's adopt it for the simple case of no cosmological constant (Lambda=0):

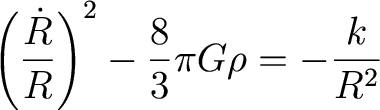
We said that if the Universe was not decelerating -- if there was no gravity to slow the expansion -- the age of the universe would simply be 1/H₀. This is the age that corresponds to a Omega=0 (or Omega very small) universe.

What about the age of a critical universe, one that has just enough mass to halt the expansion (Omega=1)? We can integrate the Friedman equation (remembering that rho ~ R^-3) to get

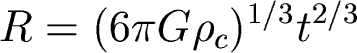
Now we use our definition of the critical density:

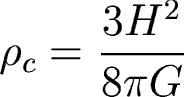
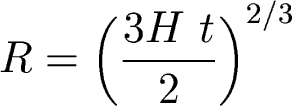
Finally, remember that we defined R such that now, R=1. So to get the age of the universe we set R=1 and solve for t, to get

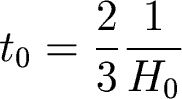
So a critical universe is 2/3 as old as an empty (or "very open") universe. So the age of the Universe depends both on the Hubble constant and the density parameter. For H₀=72 km/s/Mpc, we had that an open (empty) universe is 13.9 Gyr old, but a critical universe is only 9.3 Gyr old.

Problem: Globular clusters are old: ~ 9-12 Gyr old. How can the universe be younger than the stars it contains? It can't, driving the "Cosmological Crisis" of the early 1990s.

How to fix?

Think conceptually about what changes the R(t) curves:

• The Hubble constant is essentially the rate of change measured today: changes the R(t) slope at t₀.
• Adding density increases the rate of deceleration: makes R(t) more concave downwards

So, possible solutions:

• Reduce H₀: if H₀=50 km/s/Mpc, the ages become 20 Gyr (open) and 13 Gyr (critical).
• Throw out critical cosmologies and adopt low density "open" models.
• Throw out globular cluster age estimates.
• Add a cosmological constant ("dark energy"): lambda adds acceleration, makes R(t) concave upwards