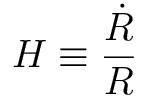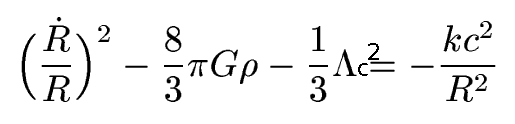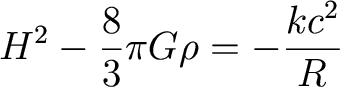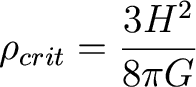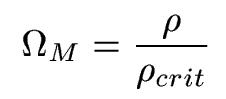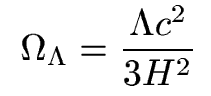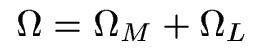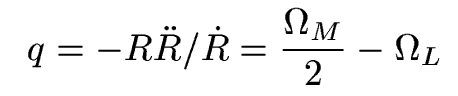Cosmological Parameters

Before going further, it is useful to define some of the cosmological parameters in the Friedmann equation (and elsewhere).

1. The Hubble Parameter

The Hubble parameter is the normalized rate of expansion:

Note that the Hubble parameter is not a constant! It changes with time. The Hubble constant is the Hubble parameter measured today -- we denote its value by H₀. Best estimates are in the range of H₀ = 65-75 km/s/Mpc. (ASTR 222 recommended value = 72)

Also note you will often see the parameter h, particularly in distance-dependant quantities (for example, 30h^-1 Mpc). This is usually defined by h=H₀/100.

2. The Matter Density Parameter.

Look at the Friedmann equation:

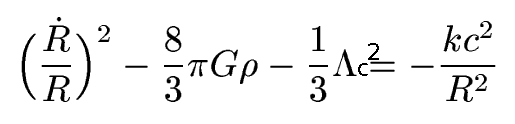
Rewriting this using the Hubble parameter, and for now set Lambda=0:

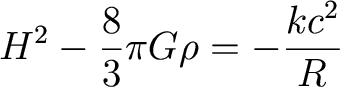
The Universe is flat if k=0, or if it has a critical mass density (in the absence of lamba) of

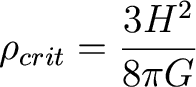
We define the matter density parameter as

Best measurements for Omega-matter are about 0.25 - 0.3, meaning the universe cannot have spatial flatness based on mass alone.

3. The "dark energy" density parameter

We can express a similar density parameter for lambda again by using the Friedmann equation and setting rhom=0. We then get

Best measurements for Omega-lambda are about 0.7-0.75

4. "Total Omega"

Questions: What is Omega if the Universe is flat? What is Omega if the Universe is accelerating?

Best estimates for total Omega are about 1.0

5. The deceleration parameter

We can make a dimensionless parameter that describes the de/acceleration rate of the Universe's expansion:

Given values above, q ~ -0.55, in other words the universe's expansion is accelerating.