Actually, it can. Solving the Einstein
field
equations
for an isotropic, homogeneous Universe yields a similar form for the
dynamics equation:
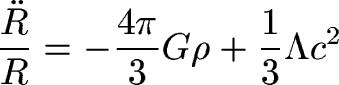
Solving this we get the equation governing the expansion of space:
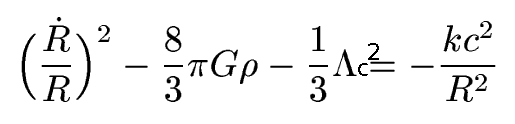

|
Actually, it can. Solving the Einstein
field
equations
for an isotropic, homogeneous Universe yields a similar form for the
dynamics equation: 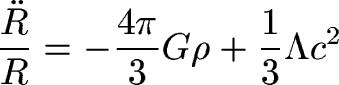 which
is what we
had before, but with an additional
term (Lambda) called the "cosmological constant" expressing the effects of "dark
energy" (the vacuum energy density of space?).
Solving this we get the equation governing the expansion of space: The Friedmann Equation
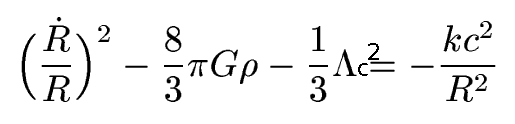 where k now corresponds
to the curvature of space.
|
 |
1. The Universe can accelerate
Look at the dynamics equation and note
that if Lambda is positive, it counteracts the deceleration due to
gravity and therefore can accelerate the expansion of the universe.
2. Space is curved
Think of our analogy of ants crawling around on an expanding balloon. Keep thinking along those lines.
We have three options for curvature:
k=1: positive curvature (like a ball)
k=0: zero curvature (flat like paper)
k=-1: negative curvature (saddle-like)

(courtesy Syracuse University)
3. Density (rho) can take on different forms, and the universe behaves differently under each one.
We made the assumption of a matter dominated Universe (so that rho ~ R-3). This was not always true in the Universe. rho is actually the inertial mass density of the matter and radiation in the Universe. If the energy density in the universe is given by U, we can convert that into an equivalent matter densityand relate it to the photon density like this So if we trace the history of the Universe back far enough, at some point the energy density of radiation exceeds that of matter, and we get to the radiation dominated era. At this point, the expansion dynamics are different, driven by radiation rather than gravity. This happens at a scale factor of R=10-3 - 10-4, so we can ignore it for the purposes of observational cosmology. But it does change the expansion rate in the early universe...
The energy density of matter and radiation drops as the universe expands. The density of dark energy does not. Eventually, Lambda wins. In this case, R ~ exp(t) -- exponential expansion.
Without lambda, spatial curvature and expansion history were locked together. With lambda, that connection is broken. Closed universes can expand forever, open universes can collapse, etc. Life becomes messy!