The Expanding Universe

1917: Willem de Sitter used general relativity to describe an expanding universe. Einstein favored a static model which neither expanded nor contracted, by inserting an ad-hoc term he called the cosmological constant.

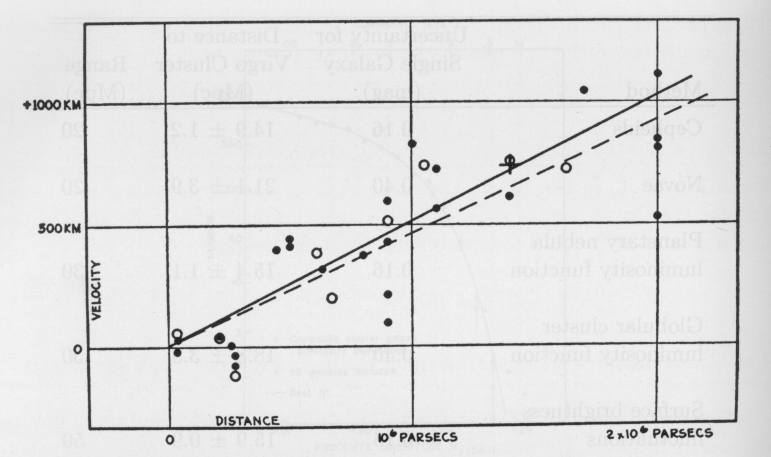
1929: Hubble measures the expansion of the Universe

We can rewrite this relationship as v=H₀d, where H₀ is the Hubble constant. Hubble's original derivation gave H₀ ~ 200 km/s/Mpc, but this is wrong because Hubble had the distances to the galaxies wrong. Modern measurements give a value more like H₀ = 72 km/s/Mpc (+/- a handful)

(Because of historic uncertainty in the Hubble constant, in the past, astronomers often defined a parameter h=H₀/100, and write distance dependant results as (for example), d=200h^-1 Mpc.)

The Cosmological Redshift

Remember the redshift:

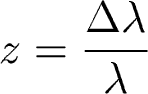
Using normal Doppler equation (v<<c), v=cz, and d=cz/H₀.

But it is important to realize here that the cosmological redshift is not really due to galaxies moving through space at high velocities. Galaxies are actually "embedded" in space and space itself is expanding. The light emitted from the galaxies is "stretched" as it makes its way towards us, and we see it shifted to longer wavelengths.

Measuring distances in an expanding universe:

The distance between two objects can be defined as d = R(t) x r, where

d = proper distance

R = dimensionless scale factor

r = comoving coordinate

For two galaxies r only changes due to peculiar motion of the galaxies (ie due to gravity in a cluster, etc). The change in proper distance due to the expansion of space is entirely contained in R(t). We define R(now) = 1.

Note that on cosmological scales, this makes the distance between two objects an ambiguous concept. There are different ways of defining distances, which give different answers.

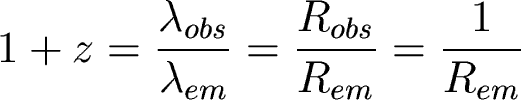
Go back to the redshift. What does that tell us about the expansion?

So if we observe a quasar at a redshift of z=3, at the time the light left the quasar, the universe was 1/4 its current size.

The Age of the Universe

As z gets large, R gets small. At some point, R=0! When did that happen?

Homer solves the age of the Universe.

Let's see. Space is expanding in such a way that d=v/H₀, then to get to a distace d moving at velocity v would take time t₀=d/v=1/H₀. So the inverse of the Hubble constant is a (rough) measure of the age. This is called the Hubble time.
If H₀ = 72 (km/s)/Mpc, this is ~ 72 (pc/Myr)/Mpc, which is 72x10^-6 Mpc/Myr/Mpc = 7.2x10^-5 Myr^-1.

Then t₀ = 1/H₀ = 1.39x10⁴ Myr = 13.9 billion years.

There's a pretty big assumption built into this -- what is it?