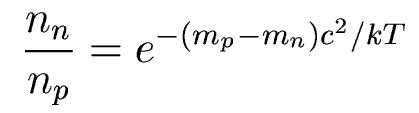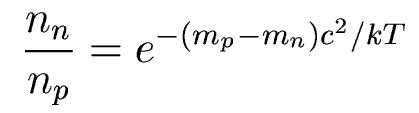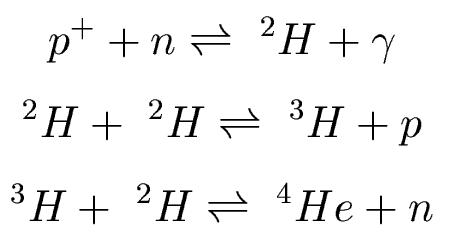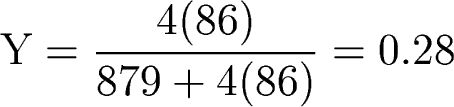Big Bang Nucleosynthesis
So we have the building blocks of the elements:
protons,
neutrons, electrons. The temperature is high, but dropping fast; the
density
is also pretty high, but also dropping fast. If we act quick, we might
be able to have nuclear fusion. This happens when the Universe is a few
minutes old.
Step 1: Initial mix of particles
When the Universe is a few seconds old, at T=1010
K, protons and neutrons are in thermal
equilibrium,
and their ratio is given by the Boltzmann
equation:
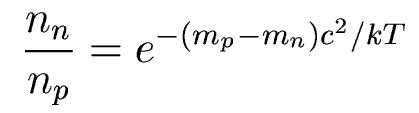
which gives n/p = 0.223. Below 1010
K, no
new
neutrons are formed, so that ratio is frozen in. Yet it is too hot for
nuclear fusion to happen, so the mix of protons and neutrons is
maintained. So
for every 1000 protons, there are 223 neutrons.
Step 2: Beta decay changes the balance
But free neutrons undergo beta
decay, which converts neutrons into protons with a half life
of 617 seconds. When the universe was about four minutes old, the time
the temperature had dropped to 109
K, and particles can begin to fuse together in nuclear reactions. At
the point in time when this happens, neutron decay has rebalanced the
neutron to proton ratio
to n/p=0.164. So our proton/neutron mix above
has changed to 1051 protons and 172 neutrons.
Step 3: Nucleosynthesis
Now we are are ready for nucleosynthesis. At 109
K, fusion of particles can create deuterium,
tritium, and helium:
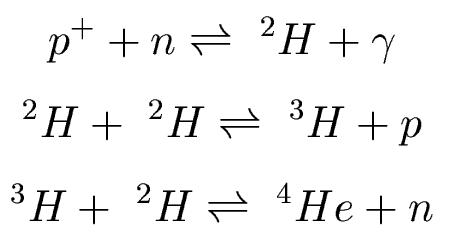
(note that these are different reactions from pp chain that powers the Sun!)
These reactions happen so efficiently that we make
as
much helium as possible. If we have 172 neutrons, we can make a total
of
86 4He nuclei, with 879 protons (H nuclei) left over. So
the
mass fraction of helium in the Universe was
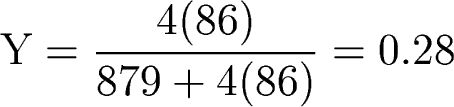
Which is not too far off the observed value of the primordial
helium content of the Universe: ~ 23-24%.
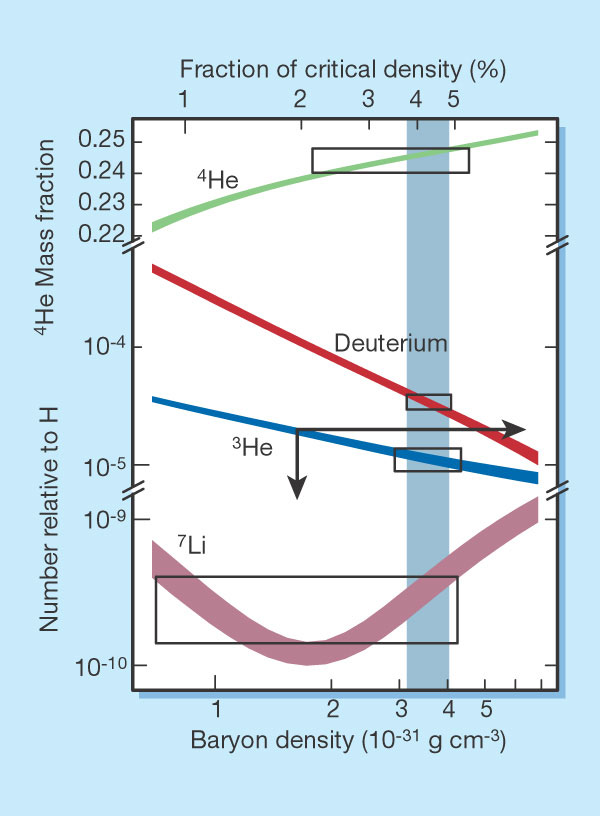
A full nucleosynthesis model looks like this:
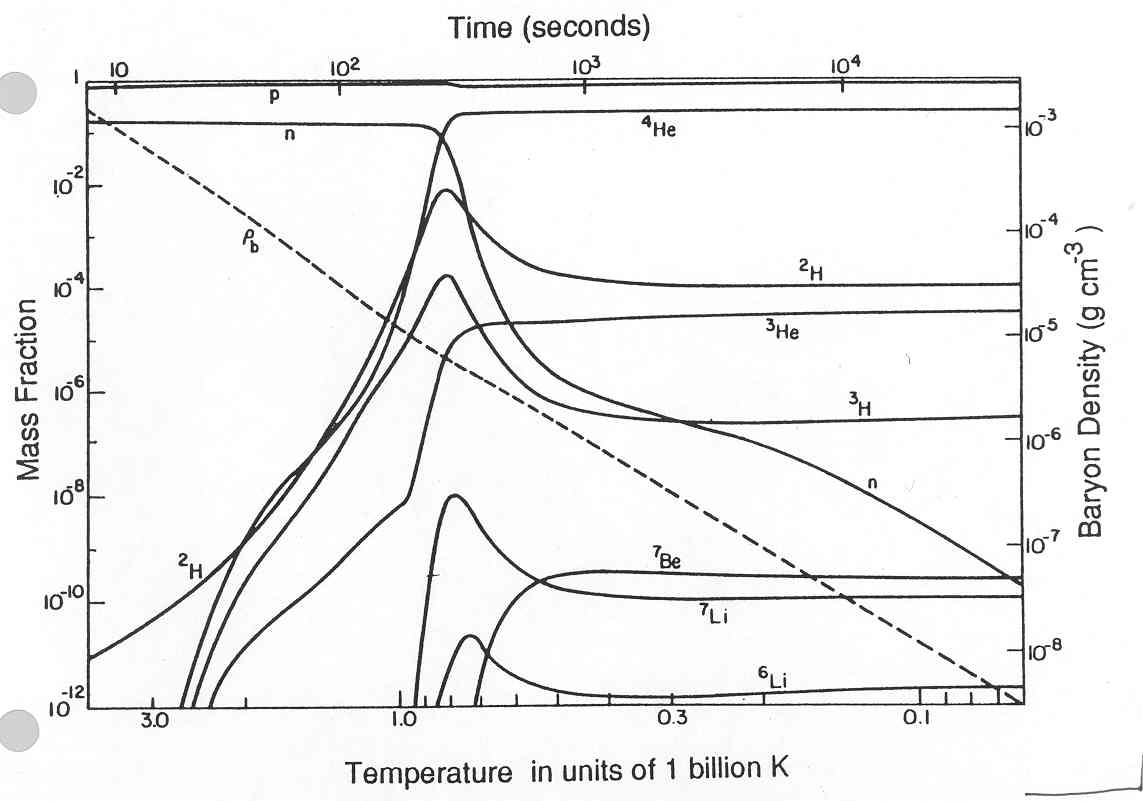
Some of the less massive
nuclei are also produced: deuterium (2H), 3He,
7Li. The
abundances of these elements can be used to constrain the baryonic
density
of the universe at the time of BBN.
If the baryon density is high, the reactions are more efficient, more 4He is created, and fewer intermediate nuclei like 2H are left over.
If the density is low, the reactions happen more slowly, and dont create as much 4He before the temperatures drop too low. More intermediate nuclei are left over.
The plot at the left shows the abundances of
these light
elements as a function of the present baryon density of the universe.
Based
on the observed abundances of these elements (particularly deuterium -- 2H), we infer that the
baryonic density of the universe is only a few percent of the critical
density.
Dark matter cannot be normal baryonic material!
|
|