![]()
![]()
If we can find Cepheids in distant galaxies and measure their brightness changes, we can in principle solve for their distance.
Problem #1: As luminous as they are, in distant galaxies Cepheids will be very faint.
Example: How bright would a Cepheid be in a galaxy 10 Mpc away? SinceProblem #2: Cepheids in distant galaxies will be difficult to pick out!m-M=5log(d) -5,
m-M=30.If the Cepheid has a period of 40 days, it has M=-5.9. So the apparent magnitude will be
(m-M)+M = 24.1. This is faint!
But with new big telescopes, we can detect objects this faint. If we can see down to m=26 (for example), that means we can see to a distance modulus of
(m-M)=(26 - -5.9) = 31.9,
which translates to a distance of 24 Mpc.
Yet the most distant ground-based Cepheid distance determination is ~ 15 Mpc (and is somewhat ratty).
Why is it hard to do?
Here is M100: find me an individual Cepheid in this
galaxy...

Solution: Use the Hubble Space Telescope. (Which problem does this solve?)
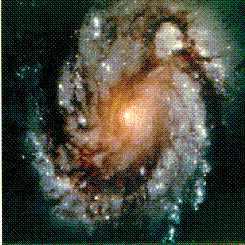
HST finds Cepheid variables in the Virgo cluster galaxy M100
And so the distance to M100 is ~ 16 Mpc.
Okay, all is peachy. But even with HST, the mirror is relatively small (2.4 meters) and crowding becomes difficult at very large distances. So we can basically measure distances out to the nearest galaxy cluster. But there's another problem with Cepheids: what kind of galaxy would you not be able to use them to get a distance to?
Remember what Type Ia supernovae are: 1.3 Msun white dwarf which suddenly ignite carbon burning in their degenerate core. When 1/2 the mass is converted into iron, they explode.
Problem #1: How do we calibrate?
We need to find the absolute distance (somehow) to a galaxy which has had an observed Type Ia supernova. The best way is to use Cepheids. Why is this a problem?Problem #2: Are SN Ia's really standard candles?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
This translates to -19.51 +/- 0.18. An dispersion of 0.18 magnitudes translates to a distance uncertainty of 10%. Not bad, but there are some whopping outliers. Can we do better?Advantage: Type Ia supernovae are bright!Yes. It turns out that the brighter SN Ia's decline more slowly than the fainter ones. Measure how bright they are and how fast they fade, and you can make a correction. This reduces the dispersion in absolute magnitude to about 0.1 magnitudes.
If we can see to m=26, that translates to a distance modulus ofOkay, let's get a distance to a galaxy with a Type Ia supernova: NGC 4639, also in the Virgo cluster. Using this technique, the distance to NGC 4639 is 25 Mpc.m-M = (26 - -19.5) = 45.5,
or a distance of 10,000 Mpc! But we can't really do quite that well -- that's the absolute magnitude at peak, and we need to measure its fading...
But wait! the Cepheids in M100 put the
distance
to Virgo at 16 Mpc. What gives?
Remember what Tully-Fisher says: luminosity and circular velocity are related (ideally, L ~ v4). If we can calibrate this, and if we can measure the circular velocity of galaxies, we can get their luminosity and distances.
Problem #1: We don't understand the physics behind Tully-Fisher!
The Tully-Fisher relationship does not go like L~v4. It has subtle but important variations onProblem #2: Calibration.
- how you measure the velocity width. What is the circular velocity of these galaxies?
- the Hubble Type of the galaxies in question (Sa vs Sc for example).
- what wavelength you measure it in.
We need to get the absolute distances to a number of spiral galaxies in order to calibrate the T-F relationship. There aren't that many big spiral galaxies around that we have Cepheid distances to.