Dynamical Distance Indicators

Tully-Fisher Relationship

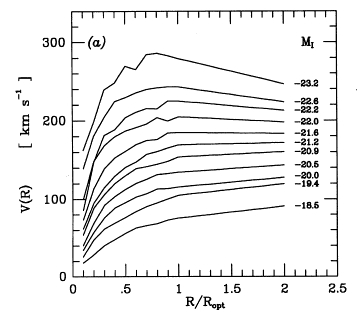
Remember what Tully-Fisher says: luminosity and circular velocity are related (ideally, L ~ v⁴). If we can calibrate this, and if we can measure the circular velocity of galaxies, we can get their luminosity and distances. (This is your homework problem #1...)

Problem #1: We don't understand the physics behind Tully-Fisher!

The Tully-Fisher relationship does not go like L~v⁴. It has subtle but important variations on

• how you measure the velocity width. What is the circular velocity of these galaxies?

• the Hubble Type of the galaxies in question (Sa vs Sc for example).
• what wavelength you measure it in.

We need to get the absolute distances to a number of spiral galaxies in order to calibrate the T-F relationship. There aren't that many big spiral galaxies around that we have Cepheid distances to.

Problem #3: What kind of galaxies does this work on? Where won't it work?

D_n-sigma

Take the fundamental plane for ellipticals. Remember how we can permute all the variables around (L, sigma, r_e, I). The fundamental plane can be permuted into:

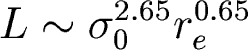
So if we measure sigma and r_e, we can get L, the luminosity. This would be one possibility.

What is more commonly done is to define D_n as the physical radius (in kpc) inside which the average surface brightness of the galaxy is 20.75 in B. Assuming the ellipticals follow the R1/4 law, we can use the fundamental plane to show that

So if we can calibrate this, then all we need to do is measure the velocity dispersion and angular size within which I=20.75. Since we know from D_n-sigma what the physical size is, we can calulate the distance. This is called a standard rod measurement.

Advantage: its a way to measure distances to a large number of ellipticals.

Disadvantage: we don't understand the physics behind the fundamental plane.

Disadvantage: how do we calibrate it?

We need to get an absolute distance to an elliptical. Why is this hard?