Left: X-ray image; right: optical image
Clusters vary greatly in properties:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We live in the Local Group :


Virgo is a spiral-rich cluster. ~ 20% of the bright galaxies are ellipticals, the rest are spirals. But the faint galaxies are mostly dwarf ellipticals...
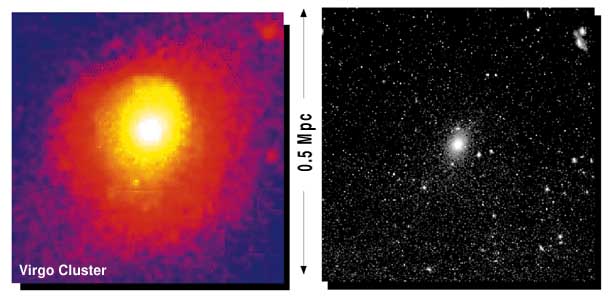
Virgo is not only filled with galaxies, but also with hot gas:
Left: X-ray image; right: optical image

Further away is a very massive cluster: the Coma cluster, at a distance of about 100 Mpc. Coma is about 6 Mpc in size and contains perhaps 10,000 galaxies. Very few of the galaxies in Coma are spiral; most are elliptical and S0.
The Coma Cluster, courtesy Adam Block

So what is the kinetic energy of the cluster? If we look at the galaxies, they would have a total kinetic energy of
where v is their full space velocity and sigma is the line of sight velocity dispersion of the galaxies in the cluster.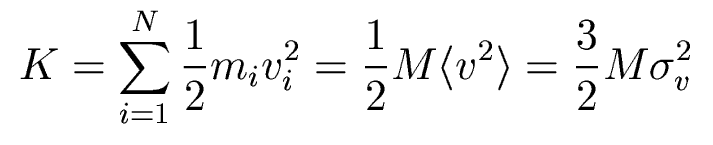
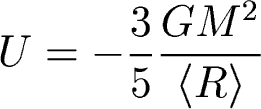
So we can solve for the total mass of the cluster:
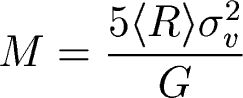
Method 2: Another way to get the mass of the cluster is to use assume the X-ray gas is in hydrostatic equilibrium (ASTR221 hydrostatic equilibrium notes). This means that the thermal pressure of the gas is in equilibrium with the gravitational potential:
Using the density and temperature of the hot gas you can then solve for the cluster mass.
Method 3: A third way of measuring the mass of the cluster is to count up all the galaxies, adopt a mass-to-light ratio for each one to determine their mass, and then tally up the mass directly.
The first two answers give reasonably consistent results. The third answer is an order of magnitude too small. What does this mean? Either: