We measure angular sizes, defined in the following way:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Okay, we can measure apparent sizes (theta). How can we get the true size (r)? Trigonometry! If we know the distance (d), we simply have r=d tan(theta).
So, how do we get a distance?
 Okay,
stick your thumb up at arm's length (Aaaayy!).
Close one eye, then the other (and open the first one, so you can still
see...). See how your thumb's position shifts relative to the background
wall? This is called parallax. Now
bring your thumb closer to your face, and do it again. The shift is bigger!
You can use parallax to measure distance. (Right,
Fonzie?)
Okay,
stick your thumb up at arm's length (Aaaayy!).
Close one eye, then the other (and open the first one, so you can still
see...). See how your thumb's position shifts relative to the background
wall? This is called parallax. Now
bring your thumb closer to your face, and do it again. The shift is bigger!
You can use parallax to measure distance. (Right,
Fonzie?)
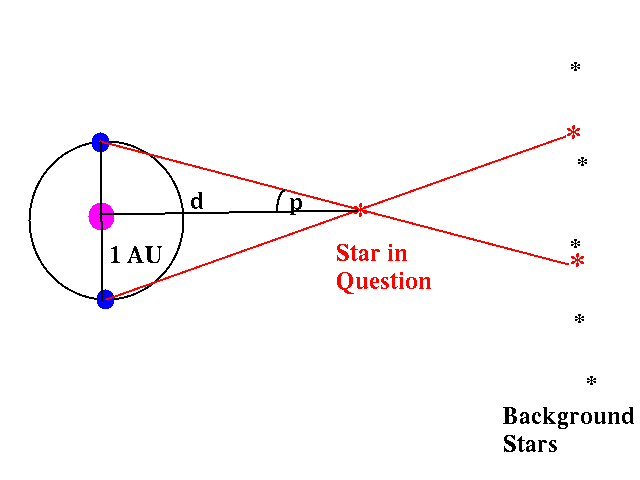
Okay, so let's do this with stars.
Instead of closing one eye and then the other, we observe a star six months apart, so that we are on opposite sides of the sun for each observation. Watch the star shift against background star field, and measure that shift. Define the parallax angle as half this shift:

Using trigonometry, we can solve for the distance. If we measure p in radians, we have:
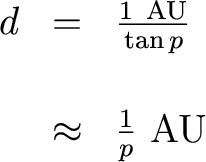
But we usually measure angles in arcseconds. Since 1 radian = 57.3o = 206265", we have
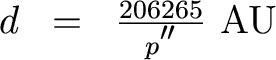
Okay, now comes the thinking part. Let's define a unit of measure called the parsec (pc) which is simply 1 pc = 206265 AU. Then we have
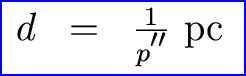
1 parsec is 3.26 light years. The nearest star has
a distance of 4.2 light years, which is 1.3 pc. Its parallax angle is 0.77"
-- small!
Stars are so distant that measuring parallax is
difficult. The smallest parallax angles which are currently measurable
are about 0.001", corresponding to a distance of 1000 parsecs (a kiloparsec).
This is much smaller than the size of our galaxy -- we can only use parallax
to measure distances of stars in the "solar neighborhood."