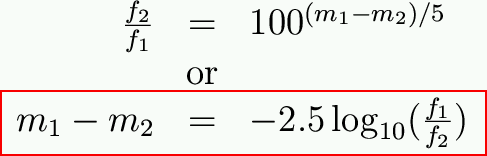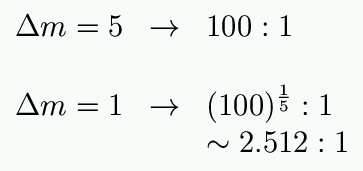
How do we define the apparent brightness of stars in the night sky? The Greek astronomer Hipparchus cataloged the stars in the night sky, defining their brightness in terms of magnitudes (m), where the brightest stars were first magnitude (m=1) and the faintest stars visible to the naked eye were sixth magnitude (m=6).
First confusing point: Smaller magnitudes are brighter!The magnitude scale was originally defined by eye, but the eye is a notoriously non-linear detector, especially at low light levels. So a star that is two magnitudes fainter than another is not twice as faint, but actually about 6 times fainter (6.31 to be exact).
Second confusing point: Magnitude is a logarithmic scale!A difference of one magnitude between two stars means a constant ratio of brightness. In other words, the brightness ratio between a 5th magnitude star and a 6th magnitude star is the same as the brightness ratio between a 1st magnitude star and a 2nd magnitude star. Are we confused yet?
So, do we toss out this confusing, archaic measure of brightness?? Absolutely not!
We refine it, and precisely define the scale such that a difference of 5 magnitudes is equal to a factor of 100 in brightness.
So what is the brightness ratio which corresponds to 1 magnitude difference?
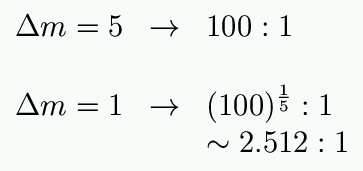
What are some magnitudes?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
What is the magnitude scale really measuring? Radiant energy flux (f) (ie ergs/s/cm2) coming from the star and hitting your detector.
Let's define things even more mathematically for the relationship between magnitude and flux from two objects (1 and 2):