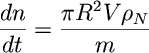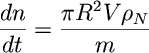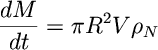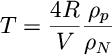ASTR221 HW#4 -- Due Oct 21 2005

1. Saturn's Rings

We will make a rough estimate of the mass contained in Saturn's rings. Assume that the rings have a constant mass density and that the rings are 30 meters thick with an inner radius of 1.5 R_Saturn and an outer radius of 3 R_Saturn. Assume also that the ring particles are water-ice spheres of radius 1 cm and that the optical depth of the rings is unity (i.e., tau=1, so you can just barely see through them).

• What is the number density of particles in the rings (how many particles per cubic meter)? So how many particles total are there?
• If water-ice particles have a density of 1000 kg/m³, what is the mass of each particle? So how much total mass is in the rings?

• If you were to take these ring particles and merge them together to make a spherical moon, how big would that moon be? How does this compare to the size of Mimas, one of Saturn's inner moons?

2. Planetary Accretion

When the solar system first formed, it was characterized by a disk of dust and gas (called the "solar nebula") with some larger planetesimals embedded within it. As these planetesimals orbited in the solar nebula, they continually accreted material from the nebula, slowly growing in size. In this problem, we will estimate how long it took these planetesimals to grow into reasonable sized objects (ie a thousand km or so in size).

• If a planetesimal has a cross-sectional area of piR² (where R is the planetesimal's radius) and is sweeping through a cloud of smaller particles of fixed size with a velocity V, show that the number of collisions per second will be

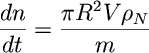
where rho_N=the space density (kg/m³) of particles in the cloud and m=the mass of each particle.

• Show that if each collision results in the target particles sticking to the planetesimal, the planetesimal will gain mass at a rate of

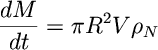
where M=the planetesimal mass.

• Show that the time to grow to radius R is

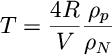
where rho_p=the density of the planetesimal itself. (Assume that rho_N and V stay constant as particles are swept up.)
• Assuming that a reasonable value for the density of accretable material in inner part of the early solar nebula is rho_N = 10^-7 kg/m³, estimate the time to accrete a body of 1,000 km radius. Assume a reasonable rho_p. Is the timescale resonable given the formation time of the planets (50 million years or so)? How does the timescale change if the accretion process is inefficient, so that not every particle sticks to the planetesimal?

3. Magnitudes and Distances

• Fill in the blanks for the stars on this table:
  

• Let's consider a (rather strange) cluster of 10,000 stars. 100 of the stars have an absolute magnitude of M=0 and the rest have an absolute magnitude of M=5. What is the total  (also known as the "integrated") absolute magnitude of the cluster? If the cluster is 3 kiloparsecs away, what is its apparent integrated magnitude?
  

4. Textbook Problems

• Problem 2.5
• A variation on Problem 2.30: If we have an uncertainty (call it "dm") in our measurement of the magnitude of a star, derive an analytic expression for the resulting relative uncertainty in the distance we derive to the star (assuming we know its absolute magnitude exactly). Note that this expression only holds if the uncertainty is relatively small.